Устойчивость прямых стержней — это одна из важнейших характеристик конструкций, подвергающихся нагрузкам. Правильный расчет устойчивости стержней позволяет предсказать их поведение при различных видах внешних воздействий и гарантировать безопасность сооружений. Особенно это важно в строительстве, машиностроении и других отраслях, где использование стержней в качестве несущих элементов является стандартной практикой.
Этот процесс включает в себя определение критической нагрузки, при которой стержень теряет устойчивость, и поиск эффективных методов для предотвращения разрушения. Важно понимать, что устойчивость стержней зависит от множества факторов, включая материал, форму, длину и условия закрепления. В данной статье будут рассмотрены основные принципы расчета прямых стержней постоянного сечения на устойчивость, а также особенности, которые влияют на эти расчеты.
Идея устойчивости стержней была сформулирована еще в XVIII веке, и одним из первых, кто рассмотрел этот вопрос с теоретической точки зрения, был Леонард Эйлер. В 1757 году он разработал теорию устойчивости для длинных цилиндрических стержней, подвергающихся компрессионной нагрузке. Теорема Эйлера стала основой для дальнейших исследований в этой области, и ее принципы используются до сих пор в инженерной практике.
После этого многие ученые, такие как Огюстен Луи Коши и другие, развивали теории устойчивости для различных типов стержней и конструкций, с учетом различных факторов, таких как различные способы закрепления, изгиб, воздействие динамических нагрузок и так далее. Современные методы расчета устойчивости учитывают эти улучшенные теории и позволяют инженерам точно прогнозировать поведение стержней в реальных условиях эксплуатации.
Основные теории и принципы расчета устойчивости стержней
Прямой стержень на устойчивость подвергается действию силы, направленной вдоль оси стержня. Если эта сила достигает определенного значения, стержень начинает деформироваться, и его ось отклоняется от первоначального положения. Потеря устойчивости происходит, когда сила превышает критическую нагрузку, после чего стержень теряет свою прямолинейность и начинает изгибаться.
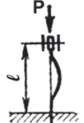
В общем случае величину критической силы Ркр , при которой прямолинейная форма стержня становится неустойчивой, определяют по формуле Эйлера:
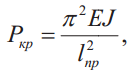
где Е — модуль продольной упругости материала стержня (модуль Юнга); J — минимальный осевой момент инерции поперечного сечения стержня; lпр — приведенная длина стержня (lпр = vl, здесь v — коэффициент приведения, зависящий от схемы нагружения и закрепления стержня, (табл. 1).
Формула Эйлера предполагает идеальные условия для стержня, включая отсутствие любых отклонений от прямолинейности, отсутствие вращений на концах и пренебрежение сжатием в других направлениях.
Критическое напряжение
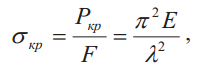
где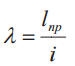 
— гибкость стержня (i — минимальный радиус поперечного сечения стержня, см. табл. 2).
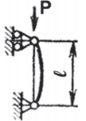
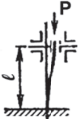
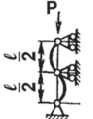
Таблица 1. Схемы нагружения и закрепления стержней
| Схема | Ркр | lпр | J | Схема | Ркр | lпр | J |
 |
 |
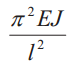l |  |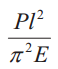
 |
 |
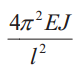0.5l |  |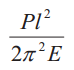
 |
 |
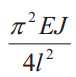2l |  |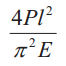
 |
 |
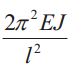0.7l |  |
 |
 |
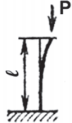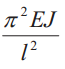l |  |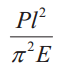
 |
 |
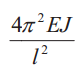0.5l |  |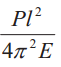
Примечание. Обозначения: Ркр — критическая сила; lпр — приведенная длина стержня; J — минимальный допустимый осевой момент инерции попереч- ного сечения стержня при силе Р.
Таблица 2. Осевые моменты, моменты сопротивления и минимальный радиус инерции профилей
 |
|||
| Эскиз | Осевой момент инерции, см4 | Момент сопротивления, см3 | Минимальный радиус инерции поперечного сечения, см |
| 1 |  |
 |
 |
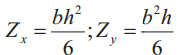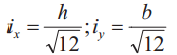| 2 |  |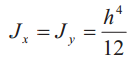
 |
 |
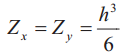| 3 |  |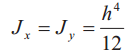
 |
 |
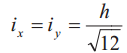| 4 |  |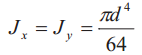
 |
 |
| 5 |  |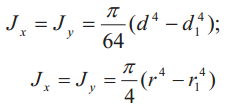
 |
 |
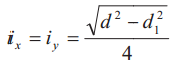| 6 |  |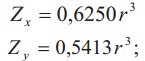
 |
 |
| 7 |  |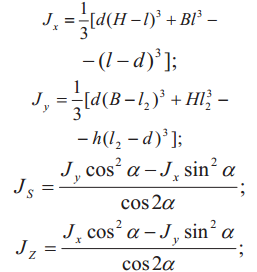
 |
 |
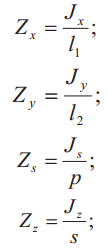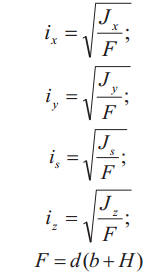| 8 |  |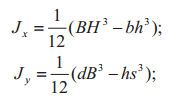
 |
 |
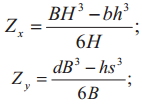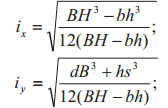| 9 |  |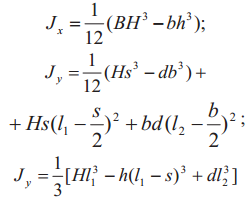
 |
 |
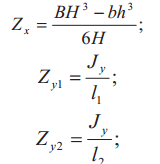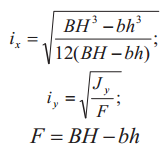Свойства материала оказывают значительное влияние на расчет устойчивости стержня. Основным параметром, который используется для определения устойчивости, является модуль упругости E. Для стержней из стали или бетона этот параметр может значительно различаться, что влияет на величину критической нагрузки.
Также важно учитывать, что многие материалы обладают неупругими или пластичными свойствами, которые могут вызвать дополнительные отклонения в процессе нагрузки. В случае таких материалов могут использоваться более сложные методы расчета, учитывающие их нелинейное поведение при деформациях.
Форма сечения стержня также влияет на его устойчивость. Например, стержень с круглым сечением будет иметь определенные характеристики устойчивости, которые отличаются от таковых у прямоугольного сечения. Момент инерции сечения — один из ключевых факторов, который зависит от геометрии, и это отражается в расчетах. Для простоты, для большинства расчетов предполагается, что сечение стержня имеет постоянные размеры по всей его длине.
В инженерной практике расчет устойчивости стержней используется для проектирования колонн, балок, мостов, а также многих других конструкций. Важно, что расчеты часто включают не только устойчивость в теории, но и воздействие внешних факторов, таких как динамические нагрузки, температурные изменения, коррозия и усталость материала.
Пример из машиностроения: при проектировании стержней в рамах автомобилей расчет на устойчивость помогает определить, какую нагрузку могут выдержать элементы кузова перед тем, как они начнут изгибаться или терять устойчивость. В строительстве расчет устойчивости колонн позволяет гарантировать их способность выдерживать большие вертикальные и горизонтальные нагрузки.
Расчет устойчивости прямых стержней постоянного сечения является важной частью инженерной практики, обеспечивающей безопасность и надежность конструкций. Он позволяет предсказать, при каких нагрузках стержень потеряет устойчивость, а также какие изменения необходимо внести в проект для предотвращения разрушений.
Современные методы расчета основываются на теории Эйлера и могут учитывать различные факторы, такие как тип закрепления, форма сечения и материальные свойства. Важно понимать, что устойчивость стержней зависит не только от их геометрических параметров, но и от внешних условий, таких как динамические и температурные воздействия.