Техническая механика охватывает широкий спектр инженерных знаний и объединяет ключевые механические дисциплины, такие как теоретическая механика, сопротивление материалов, теория машин и механизмов, детали машин, а также основы конструирования. Эти области тесно связаны и формируют базу для проектирования, анализа и оптимизации самых разнообразных технических систем.
Теоретическая механика, являясь частью этой дисциплины, представляет собой науку, исследующую фундаментальные законы механического движения и взаимодействия тел. Законы, лежащие в её основе — классическая механика Ньютона, сформулированная на основе многовекового экспериментального опыта и инженерной практики.
Современные технологии, характеризующиеся высоким уровнем автоматизации и механизации, требуют от инженеров глубокого понимания процессов движения, деформации и передачи энергии. Машины, приборы, механизмы — всё это создаётся и функционирует в строгом соответствии с принципами механики. Без этих знаний невозможно не только проектирование, но и грамотная эксплуатация и обслуживание оборудования.
К ключевым задачам механики относятся:
- изучение универсальных законов равновесия и устойчивости тел;
- разработка методов расчёта конструкционных элементов на прочность, деформативность и устойчивость;
- анализ характеристик движения и взаимодействия тел в пространстве и времени;
- исследование особенностей машин и механизмов, их конструктивных решений и сфер применения.
Зарождение механики как науки уходит корнями в античность. Ещё Архимед (III в. до н. э.) исследовал равновесие рычагов, винтовую передачу и гидростатику. В Средние века труды Аристотеля дополнялись и пересматривались, однако именно с работ Галилея начинается систематизация понятий ускорения и инерции. Подлинный научный прорыв произошёл в XVII веке с формулировкой Исааком Ньютоном трёх законов движения и закона всемирного тяготения, ставших основой классической механики.
В XVIII–XIX веках механика стала важнейшей прикладной дисциплиной в инженерии. Работы Эйлера, Лагранжа, Дарбу, Ламе и Кулибина заложили основы современного инженерного расчета. С развитием промышленной революции и машинного производства потребовалось систематизировать расчёты прочности, износостойкости, передачи движения, что дало толчок к формированию технической механики как комплексной инженерной науки.
Механика, наряду с физикой и математикой, оказывает значительное влияние на развитие инженерного мышления. Она не только формирует логический подход к решению задач, но и открывает путь к осмыслению множества физических процессов, происходящих в реальной жизни. Особенно важным является то, что механика описывает наиболее простую, но фундаментальную форму движения материи — механическое движение.
Под механическим движением понимается изменение положения тела по отношению к другому телу в пространстве с течением времени. Это определение позволяет описывать поведение как отдельных тел, так и целых систем, взаимодействующих между собой.
Не менее важным является понятие механического взаимодействия — процесса, при котором тела оказывают влияние друг на друга, вызывая изменение характера движения или изменение формы тел (деформацию).
Методологическая база технической механики развивает у студентов и инженеров способность формулировать и решать прикладные задачи, используя аналитический аппарат и инженерные допущения. Это необходимо для построения моделей, расчётов и выбора рациональных решений в процессе проектирования и эксплуатации оборудования.
Таблица 1. Основные параметры механизмов и машин и их обозначение в механике
| Параметр | Обозначение |
| Характеристики ведущих звеньев: диаметр, скорость по окружности, угловая скорость, мощность, момент вращения | d1, v1, ω1, Р1, M1 |
| Параметры ведомых звеньев на соответствующем валу | d2, u2, ω2, Р2, M2 |
| КПД одного элемента, а также общий коэффициент полезного действия системы с n ступенями | η = Р2/Р1 ηобщ = η1 η2 … ηn |
| Окружная линейная скорость для ведущего или ведомого звена (в м/с) | v = ωd/2 |
| Формулы для угловой скорости (в рад/с) | ω = πn/30 = 2v/d |
| Передаваемое усилие по окружности (в ньютонах) | Ft = Р/v |
| Момент вращения (в Н·м) | Т = Р/ω = Ft d/2 = 9,55Р/n |
| Коэффициент передачи между элементами механизма | u12 = ω1/ω2 = n2/n1 u12 = Т2/Т1 = Р2ω1/Р1ω2 = Т2/(ηТ1) |
| Передаточное число цепной передачи | u = ω1/ω2 = z2/z1 |
| Общее передаточное отношение механизма с несколькими ступенями | uобщ = u1 u2 … un |
| Передаточное число зубчатого зацепления | u = z2/z1 |
| Расчёт делительного диаметра прямозубого зубчатого колеса | d2 = z2m |
| Делительный диаметр колеса с косыми зубьями | d2 = z2m/соsβ |
| Диаметр окружности деления ведущей звездочки | d2 = t/sin (180/z) |
| Мощность двигателя (Вт), необходимая с учётом потерь | Рд ≥ Р = Тω/η = Fv/η |
Таблица 2. Параметры движения в механике
|
Прямолинейное |
|
|
Обозначения: s — путь, м; t — время, с; vt — скорость, м/с; а — ускорение, м/с2; g — ускорение свободного падения, м/с2; v0 — начальная скорость, м/с |
|
| Параметры | Формулы |
| равномерное |  |
| равномерно-ускоренное (v0 = 0) |  |
| равномерно-ускоренное (v0 ≠ 0) |  |
| равномерно-замедленное |  |
| Свободное падение —
(равномерно-ускоренное) |
 |
|
Вращательное |
|
|
Обозначения: аt — угловой путь, пройденный радиусом r за время t, рад; t — время, с; ωt — угловая скорость, 1/с; ε — угловое ускорение, 1/с2; n — частота вращения, мин-1; v — линейная скорость на радиусе r, м/с; ω0 — начальная угловая скорость, 1/с |
|
| равномерное |  |
| равномерно-ускоренное (v0 = 0) |  |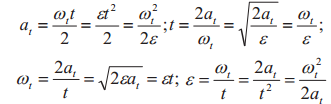
| равномерно-ускоренное (v0 ≠ 0) |  |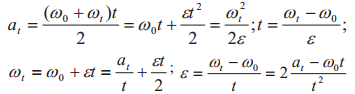
| равномерно-замедленное |  |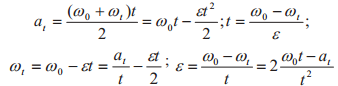
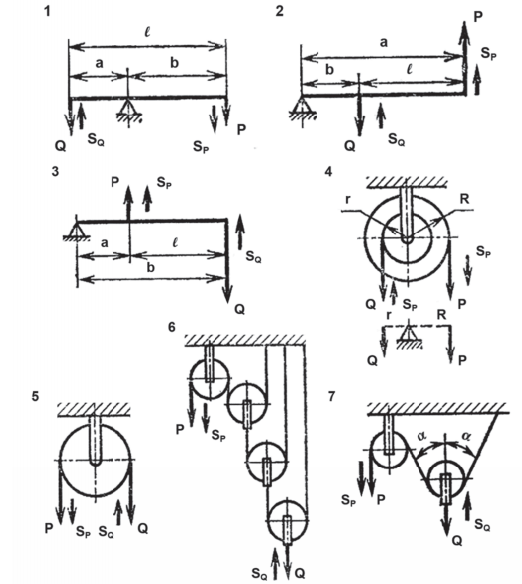
Таблица 3. Расчет сил простейших механизмов (без учета трения)
|
Рычаги и блоки |
|||
 |
|||
| Эскизы | Механизмы | Формулы | |
| Силы | Перемещения | ||
| 1 | Рычаг первого рода |  |
 |
| 2, 3 | Рычаг второго рода |  |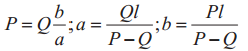
 |
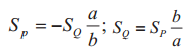| 4 | Ворот |  |
 |
| 5 | Блоки |  |
 |
| 6 |  |
 |
|
| 7 |  |
 |
|
Таблица 4. Расчет сил простейших механизмов (без учета трения)
| Винтовые и клиновые механизмы | |||
 |
|||
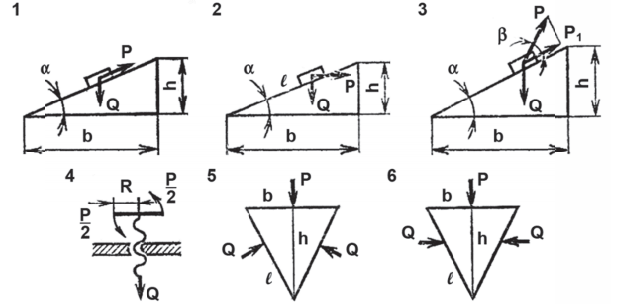| Эскизы | Формулы | Эскизы | Формулы |
| 1 |  |
4 |  |
| 2 |  |
5 |  |
| 3 |  |
6 |  |
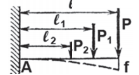
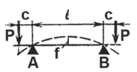
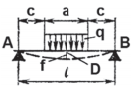
Таблица 5. Расчет балок под нагрузкой
| Схема нагружения | Реакции опор
Изгибающий момент |
Допускаемая
нагрузка |
Максимальный
прогиб |
Опасное
сечение |
 |
 |
 |
 |
А |
 |
 |
 |
 |
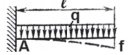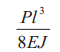А |
 |
 |
— |  |
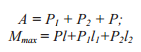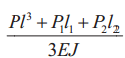А |
 |
 |
 |
 |
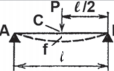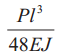C |
 |
 |
 |
 |
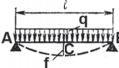C |
 |
 |
 |
 |
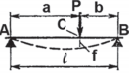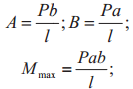C |
 |
 |
 |
 |
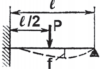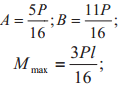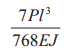А |
 |
 |
 |
 |
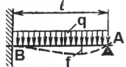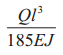B |
 |
 |
 |
 |
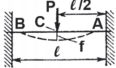А,B,C |
 |
 |
 |
 |
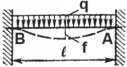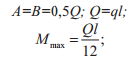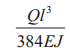А,B,C |
 |
 |
 |
 |
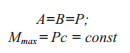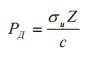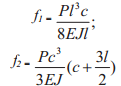Все сечения |
 |
 |
 |
 |
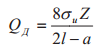D |
Интересные факты:
-
Первая инженерная задача, решённая аналитически, касалась расчёта устойчивости колонны (проблема Эйлера, 1757 г.).
-
Термин «деталь машины» как самостоятельная дисциплина был впервые введён в начале XX века на инженерных факультетах Германии и России.
-
Формулы зубчатого зацепления, актуальные до сих пор, были выведены в XIX веке и практически не изменились.
-
Принцип виртуальных перемещений, используемый в теоретической механике, применяется также в методе конечных элементов (МКЭ), который лежит в основе современных инженерных симуляций.
-
Большинство САПР и CAE-систем, таких как SolidWorks, ANSYS и Autodesk Inventor, используют внутренние модули, основанные именно на классической технической механике и её формулах.
Заключение
Механика — это не только наука, лежащая в основе большинства инженерных дисциплин, но и мощный инструмент анализа и предсказания поведения технических систем. Знание ключевых формул, обозначений и расчётных параметров позволяет инженеру уверенно проектировать надёжные, безопасные и эффективные конструкции.
Современное инженерное мышление формируется на базе строгих законов механики и математического аппарата, способного охватить как простые элементы, так и сложные многоступенчатые системы. Регулярное использование справочных данных по механике позволяет минимизировать ошибки, ускорить расчёты и принять обоснованные технические решения.
Регулярно публикую материалы о передовых методах обработки и сварки материалов, а также освещаю новинки в сфере производства,материаловедения, строительства и др.