Содержание страницы
Современная наука о материалах невозможно без глубокого понимания структуры вещества на атомном уровне. Металлы, будучи основой большинства конструкционных материалов, обладают уникальными свойствами, которые напрямую зависят от их внутреннего строения — кристаллической решетки. Именно закономерное расположение атомов в кристалле определяет такие характеристики, как прочность, пластичность, электропроводность и теплопроводность. Однако реальный металл — это не идеальный кристалл: в нем присутствуют различные дефекты, играющие ключевую роль в процессах упрочнения, разрушения, диффузии и фазовых превращений.
Цель данной работы — систематизировать сведения об атомно-кристаллической структуре металлов, рассмотреть типы кристаллических решеток, основные кристаллографические направления и плоскости, а также классифицировать возможные дефекты и их влияние на свойства материалов.
Исследования кристаллической структуры начались в XIX веке и тесно связаны с развитием рентгеноструктурного анализа. В 1912 году немецкий физик Макс фон Лауэ впервые доказал, что кристаллы могут дифрагировать рентгеновские лучи. В 1913–1914 годах отец и сын Уильям Генри и Уильям Лоренс Брегги разработали уравнение Брегга, позволившее вычислять параметры кристаллической решетки. Позже, в XX веке, благодаря развитию электронной микроскопии стало возможно напрямую наблюдать дефекты в кристаллических решетках.
Научная основа современной кристаллографии легла в фундамент металлургии, физики твердого тела и инженерии материалов. Эти открытия позволили понять природу упрочнения металлов, механизмы пластической деформации и термической обработки.
1. Кристаллическая структура металлов
Понятие атомно-кристаллической структуры охватывает пространственное упорядочение атомов или ионов, характерное для вещества в кристаллическом состоянии.
Металлы в твердом агрегатном состоянии формируют структуру, в которой положительно заряженные ионы погружены в электронное облако, состоящее из свободных, коллективизированных электронов. Эти электроны движутся между ионами, обеспечивая специфический тип связи – электростатическое взаимодействие.
Такой тип связи обусловлен действием сил притяжения между ионами и свободными электронами, формирующими общее электронное облако (рис. 1, а). Этот вид связи получил название металлической.
Равновесное положение ионов в металлическом кристалле достигается за счёт баланса между силами взаимного притяжения и отталкивания, что приводит к минимальной потенциальной энергии системы.
Ионы (или атомы) располагаются в строго определённом порядке, формируя кристаллическую решетку (рис. 1, б), которая соответствует наиболее стабильной конфигурации с минимальной энергией.
Кристаллическая решетка металла (рис. 1, б) представляет собой совокупность условных плоскостей и линий, проходящих через узловые точки, где расположены атомы. На рисунке жирной линией обозначен элемент решетки – минимальный параллелепипед, с помощью последовательного повторения которого можно воспроизвести весь объем кристалла.
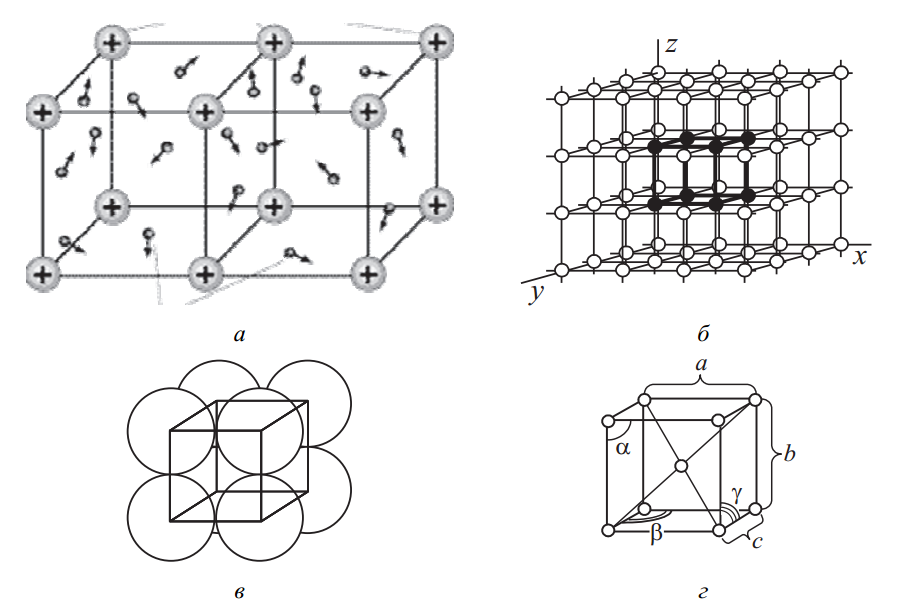
Рис. 1. Расположение атомов (ионов): а, б – в кристаллической решетке; в, г – в элементарной кристаллической ячейке
Указанный элементарный объем вещества, который полностью отображает внутреннее строение кристаллической структуры металла, называется элементарной кристаллической ячейкой (рис. 1, в, г).
Для описания элементарной ячейки требуется указание следующих геометрических параметров: три линейные величины – a, b, c, обозначающие длины её рёбер, и три угла между ними – α, β, γ (рис. 1, г).
Металлы, как правило, формируют кристаллические решетки с высокой симметрией, в которых плотная упаковка атомов достигается в одной из трёх форм: гексагональной, кубической гранецентрированной и кубической объемноцентрированной (см. рис. 2).
Гексагональная плотноупакованная структура (ГПУ) (рис. 2, а) предполагает размещение атомов в вершинах и центре шестиугольных оснований призмы, а также в центральной горизонтальной плоскости. Эта структура характерна для таких металлов, как Mg, Tiα, Zn, Be, Cd, Re, Ru, Os, Coβ, Caβ и других.
В гранецентрированной кубической решетке (ГЦК) (рис. 2, б) атомы размещаются как в вершинах куба, так и в центрах всех его граней. Металлы с такой решеткой включают Ag, Cu, Ni, Au, Pt, Rh, Pb, Feγ, Coα и др.
На рисунке 2, в представлена объемноцентрированная кубическая решетка (ОЦК), для которой характерно расположение атомов в вершинах и один атом строго в центре куба. К этой структуре относятся такие металлы, как W, V, Feα, Tiβ, Cr, Nb, Ba, Na, K, Li, Zrβ и др.
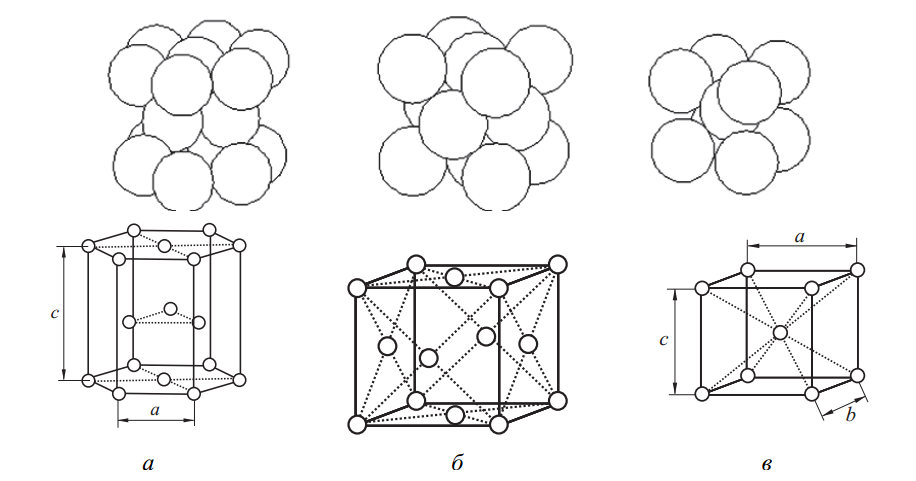
Рис. 2. Кристаллические решетки металлов: а – гексагональная плотноупакованная (ГПУ); б – гранецентрированная кубическая (ГЦК); в – объемноцентрированная кубическая (ОЦК)
Расстояния между ближайшими атомами в пределах одной ячейки – a, b и c (рис. 1, г) – называются периодами решетки. Эти величины измеряются в нанометрах: 1 нм = 10-8 мм.
Для большинства известных металлов значения периодов решетки находятся в диапазоне от 0,1 до 0,7 нм.
Количество атомов, приходящееся на одну элементарную ячейку, зависит от типа решетки. В случае ОЦК на ячейку приходится два атома: один расположен в центре куба, а суммарный вклад восьми вершинных атомов составляет ещё один (1/8 · 8).
Для ГЦК структура усложняется: один атом вносят вершины (аналогично ОЦК), а три – грани куба, где каждый гранный атом делится между двумя ячейками (1/2 · 6 = 3). Итого – четыре атома на ячейку.
Гексагональная решетка содержит шесть атомов на ячейку: 3 центральных, 12 вершинных (по 1/6) и 2 атома с плоских оснований (по 1/2).
Таким образом, знание типа решетки, размеров элементарной ячейки и числа атомов в ней полностью определяет пространственное распределение частиц в кристалле. Дополнительно к этому используются такие параметры, как координационное число и коэффициент компактности.
Координационное число определяет количество ближайших атомов-соседей. Для ОЦК оно составляет 8 (К8), а для ГЦК – 12 (К12), как видно из схемы на рис. 3.
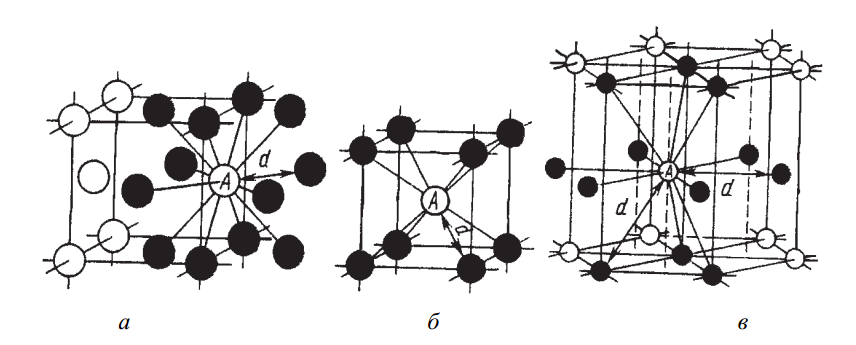
Рис. 3. Схема, показывающая число атомов, находящихся на наименьшем расстоянии от данного атома А в разных кристаллических решетках: а – ГЦК; б – ОЦК; в – ГПУ
Плотность упаковки частиц в ячейке характеризуется коэффициентом компактности, который показывает, какую часть объема ячейки занимают сами атомы. Для ОЦК он составляет 0,68, а для более плотноупакованных структур – ГЦК и ГПУ – этот показатель равен 0,74.
2. Кристаллографические направления и плоскости
Упорядоченное размещение атомов в структуре кристаллической решетки дает возможность выделить определенные кристаллографические плоскости и направления, которые играют важнейшую роль в описании свойств и поведения монокристаллов.
Кристаллографическое направление представляет собой воображаемую прямую линию или луч, выходящий из определенной исходной точки (например, вершины куба), вдоль которой атомы располагаются на равных промежутках. Примерами таких направлений служат как ребра, так и диагонали кубических граней (рис. 4, а). Кроме того, исследователями часто рассматриваются и иные направления, представляющие интерес при анализе материалов.
Кристаллографические плоскости — это геометрические плоскости, в которых атомы располагаются упорядоченно. К таким плоскостям относятся как грани куба, так и диагональные поверхности, проходящие через определенные атомные узлы (рис. 4, б, в, г).
Для определения и описания как направлений, так и плоскостей применяются специальные условные обозначения, известные как индексы Миллера. Индексы позволяют формализованно описывать ориентацию внутри кристаллической структуры.
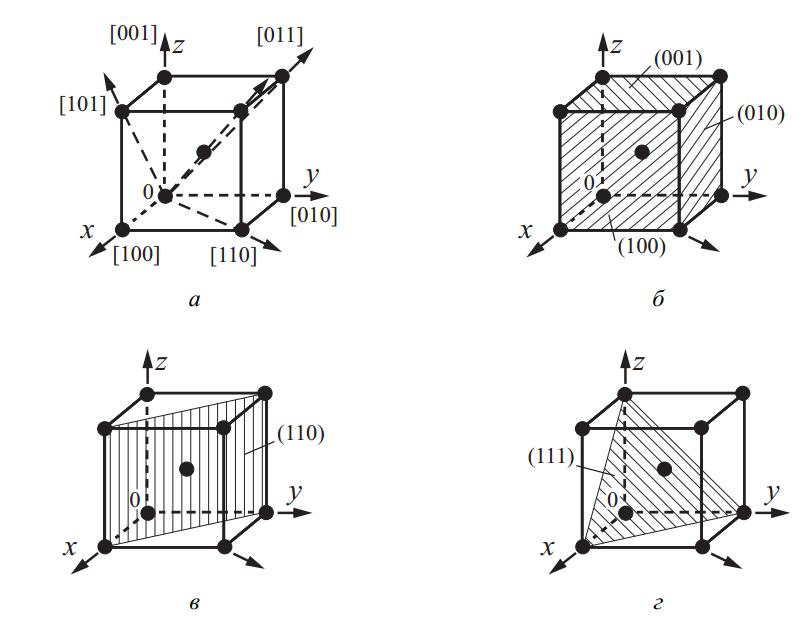
Рис. 4. Основные кристаллографические направления (а) и плоскости (б, в, г) в ОЦК-решетке
К примеру, при определении индекса направления следует взять координаты ближайшего атома, лежащего вдоль заданного направления, и выразить их через параметр решетки. Если ближайший атом расположен вдоль оси 0x, то его индекс — [100].
Соответственно, направления вдоль осей 0y и 0z получат обозначения [010] и [001]. Атомные направления, лежащие по диагоналям граней, таких как x0y, x0z, y0z и главной диагонали куба, будут обозначаться как [110], [101], [011] и [111] соответственно (рис. 4, а).
Переходя к определению индексов плоскостей, сначала необходимо определить, в каких точках плоскость пересекает координатные оси, а затем взять обратные величины этих координат. Полученные значения записываются в круглых скобках.
Например, плоскость, параллельная x0y (верхняя грань куба, рис. 4, б), не пересекается с осями x и y (расстояние бесконечно), а с осью z пересекается на расстоянии одного параметра. Это дает индекс (001).
Плоскости, параллельные осям x0z и y0z, получают обозначения (010) и (100) соответственно (рис. 4, б). Вертикальная диагональная плоскость обозначается (110), а плоскость, проходящая через все три оси координат на расстоянии одного параметра решетки, обозначается как (111) (рис. 4, в, г).
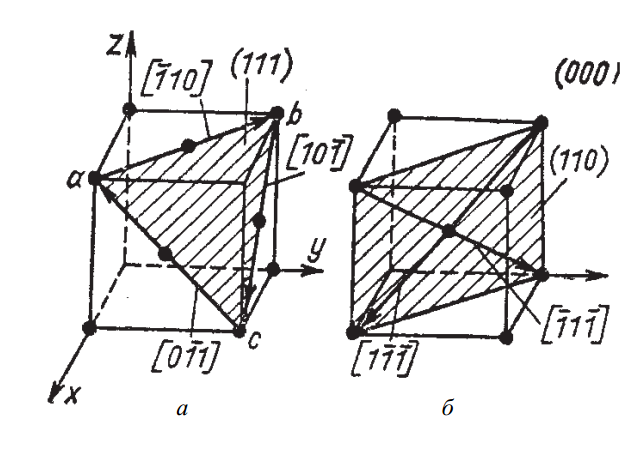
Рис. 5. Обозначение кристаллографических плоскостей куба и различных кристаллографических направлений: а – ГЦК-решетка; б – ОЦК-решетка
Понимание и использование индексов плоскостей и направлений имеет решающее значение для анализа множества явлений в кристаллах. Эти обозначения позволяют точно описывать различия в свойствах материалов вдоль различных векторов внутри кристаллической структуры.
Такие характеристики, как твердость, теплопроводность, упругость и электропроводность, зависят от плотности упаковки атомов в соответствующих направлениях. Именно по этой причине свойства одного и того же монокристалла могут изменяться в зависимости от ориентации вырезанного образца. Это явление известно как анизотропия.
Анизотропия является прямым следствием неравномерного распределения атомов по различным кристаллографическим направлениям и плоскостям. К примеру, в объемноцентрированной кубической (ОЦК) решетке плоскость (100) включает лишь один атом (суммарно: 1/4 × 4), тогда как в плоскости (110), соответствующей граням ромбического додекаэдра, находятся уже два атома: один за счет вершин и еще один из центра куба.
В случае гранецентрированной кубической (ГЦК) решетки наиболее плотно упакованной является плоскость (111), соответствующая граням октаэдра (рис. 5, а). А для ОЦК-решетки — это плоскость (110), как видно на рис. 5, б.
Из-за направленной структуры кристаллы считаются анизотропными объектами, тогда как аморфные материалы (стекло, некоторые полимеры и др.) демонстрируют изотропное поведение — их свойства одинаковы во всех направлениях и не зависят от ориентации.
3. Дефекты кристаллической решетки металлов
Большинство металлов, используемых в технических целях и в промышленном производстве, представляют собой поликристаллические материалы. Их внутренняя структура далека от идеала — атомы в кристаллической решетке распределены не строго упорядоченно, а с различными нарушениями. Эти нарушения носят название дефектов кристаллической решетки и классифицируются в зависимости от их геометрических характеристик на следующие категории: нульмерные (точечные), одномерные (линейные), двумерные (поверхностные) и трехмерные (объемные).
Точечные нарушения структуры являются дефектами, ограниченными в пространстве по всем осям. Их размеры, как правило, не превышают нескольких диаметров атома. Среди них можно выделить три основные группы: вакансии, атомы, находящиеся не в своих положениях, и примесные атомы.
Вакансии — это своеобразные «пустоты» в решетке, возникающие из-за отсутствия атомов в определённых узлах (рис. 6, а). Этот тип дефекта был подробно описан Я. И. Френкелем, который обозначил такие пустоты термином «дырки».
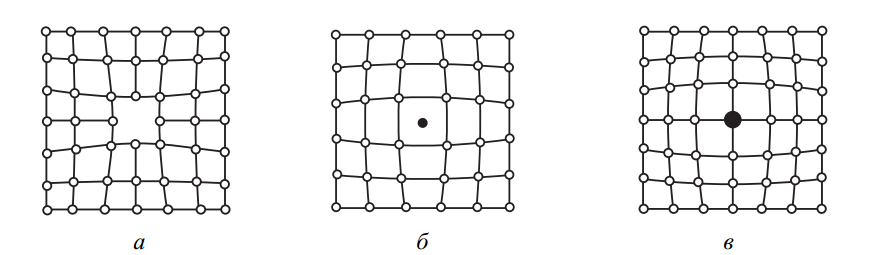
Рис. 6. Точечные несовершенства: а – вакансии; б – дислоцированный атом; в – атом примеси
Следующий тип – дислоцированные атомы – возникает, когда атом покидает своё регулярное место в решетке и смещается в междоузлие (рис. 6, б). Такие перемещения требуют значительной энергии, например, при воздействии высокоэнергетических частиц (радиация). При этом на его прежнем месте возникает вакансия — механизм, также описанный Френкелем.
Примесные атомы неизбежно присутствуют, поскольку добиться абсолютно чистого состава металла невозможно. Эти посторонние атомы могут замещать атомы основного вещества или внедряться в промежутки решетки (рис. 6, б, в), формируя так называемые замещающие и внедренные примеси.
Наличие вакансий, дислоцированных или примесных атомов всегда приводит к локальному искажению кристаллической симметрии и нарушению равномерности межатомных сил, однако эти искажения распространяются на весьма ограниченную область — в пределах нескольких атомных расстояний.
Теперь рассмотрим линейные дефекты, которые простираются в одном измерении и имеют ограниченные размеры в других двух. Главные представители этой категории — краевые и винтовые дислокации (рис. 7).
Краевая дислокация — это линия, вдоль которой в кристаллической решетке внедрена лишняя полуплоскость атомов, как видно на схеме (рис. 7, а). Эти искажения порождают упругие напряжения, распространяющиеся от линии дислокации.
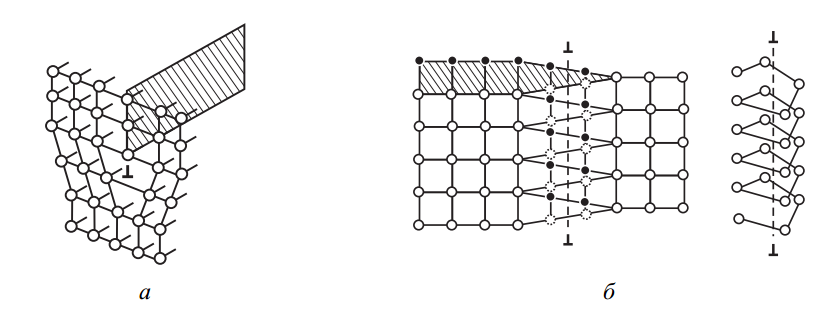
Рис. 7. Схемы краевой (а) и винтовой (б) дислокаций
Линии с одинаковой направленностью отталкиваются, а встречные — притягиваются. Эти взаимодействия определяют механические характеристики материала.
Плотность дислокаций, определяемая как совокупная длина дислокационных линий в единичном объеме, может существенно отличаться в зависимости от условий. Например, в полупроводниках плотность составляет около 104–105 см-2, в рекристаллизованных металлах — 106–108 см-2, а при значительной пластической деформации возрастает до 1011–1012 см-2. Если же плотность превышает 1012 см-2, это часто приводит к образованию микротрещин и разрушению кристаллической структуры.
Дислокации формируются как в процессе затвердевания, так и при внешних механических воздействиях. Их присутствие существенно сказывается на пластичности и прочности материала. Они же играют роль в фазовых переходах, изменяя условия роста и трансформации зерен.
Примеси, особенно внедряющиеся атомы, часто концентрируются вдоль дислокационных линий, снижая упругие искажения и повышая стабильность решетки. Также стоит отметить, что диффузия вдоль таких линий протекает в десятки и сотни раз быстрее, чем через идеально упорядоченный участок решетки.
Поверхностные дефекты характерны для поликристаллических материалов, в которых множество отдельных кристаллов (зерен) соединены между собой. Их кристаллографическая ориентация различается, и на границах между зернами образуются специфические структуры (рис. 8, а, б).
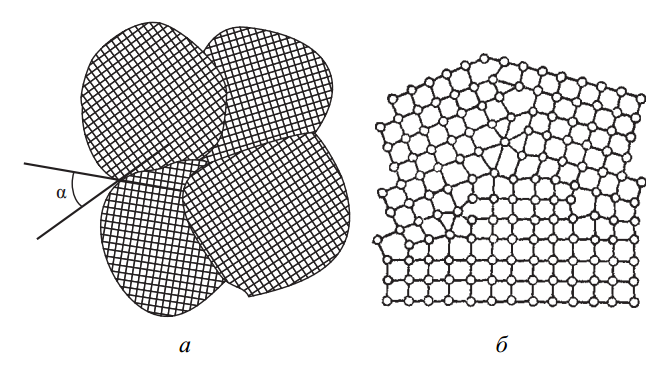
Рис. 8. Схема строения поликристалла: а – большеугловые границы между зернами; б – переходный слой (граница)
Эти границы, как правило, представляют собой тонкие (~1–5 нм) переходные области, где атомная структура нарушена, сконцентрированы дефекты, такие как дислокации, и присутствует повышенное содержание примесных элементов. Такие границы называются большеугловыми, поскольку между соответствующими кристаллографическими направлениями соседних зерен образуются значительные углы.
Рис. 9. Схема блочной (мозаичной) структуры зерен
Кроме того, каждое зерно может содержать в себе блоки или субзерна — области с близкой, но не идентичной ориентацией. Эти субзерна разделены стенками, состоящими из цепочек дислокаций. Углы между соседними субзернами невелики, и такие границы называются малоугловыми. Однако и они способны улавливать и накапливать примеси.
Механические и физические характеристики металлов, таких как прочность, вязкость и сопротивление разрушению, во многом зависят от наличия и характера поверхностных дефектов. Мелкозернистая структура увеличивает сопротивление пластической деформации и повышает долговечность изделия. Быстрая диффузия по границам зерен и субзерен особенно заметна при повышенных температурах, что важно при термической обработке и эксплуатации в агрессивных условиях.
Заключительно стоит отметить, что взаимные перемещения, взаимодействия и концентрационные изменения всех типов дефектов определяют, как поведёт себя металл в различных условиях. Именно от этих микроскопических отклонений во многом зависят макроскопические свойства конструкционных материалов.
Заключение
Интересные факты:
-
Золото и медь обладают одной и той же кристаллической решеткой (гранецентрированная кубическая), что объясняет их схожую пластичность и ковкость.
-
Алюминий при своей легкости обладает высокой прочностью именно благодаря плотной упаковке атомов в ГЦК-решетке.
-
Дефекты кристаллической решетки, несмотря на свою «ошибочность», нередко улучшают механические свойства металлов. Например, закалка стали повышает ее прочность именно за счет увеличения плотности дислокаций.
-
Анизотропия свойств кристаллов используется в ювелирной огранке драгоценных камней — знание направлений наименьшей и наибольшей прочности помогает придать кристаллу нужную форму.
-
Модернизация сплавов зачастую происходит через контролируемое внедрение примесных атомов, создающих точечные дефекты и изменяющих физические свойства материала.
Атомно-кристаллическая структура является фундаментом, определяющим поведение и свойства металлов на всех уровнях — от микроскопического до макроскопического. Понимание кристаллических решеток, типов направлений и плоскостей, а также природы дефектов позволяет инженерам и ученым эффективно управлять свойствами материалов для создания более прочных, легких, устойчивых и надежных конструкций. Современные технологии в металлургии, наноинженерии и материаловедении невозможно представить без глубокой кристаллографической базы. Таким образом, знания о структуре металлов остаются неотъемлемым звеном прогресса в науке и технике.
