Содержание страницы
Аддитивные технологии, зародившиеся в 1980-х годах с изобретением стереолитографии, произвели настоящую революцию в производстве. Переход от «вычитающих» методов (фрезеровка, токарная обработка) к «добавляющим» открыл беспрецедентные возможности для создания изделий сложнейшей геометрии. С появлением в 1990-х годах технологий работы с металлами, таких как селективное лазерное плавление (СЛП, Selective Laser Melting — SLM), индустрия получила инструмент для прямого производства функциональных, высоконагруженных деталей.
Однако, несмотря на стремительное развитие, широкое внедрение аддитивного производства в ответственные отрасли, такие как авиакосмическая и медицинская, сталкивается с серьезным препятствием. Речь идет о сложности прогнозирования финальных механических свойств изделия и необходимости проведения дорогостоящих и длительных натурных экспериментов для подбора оптимальных технологических режимов. Создание «цифрового двойника» — высокоточной математической модели, способной предсказать результат еще до начала печати, — стало ключевой задачей для современной инженерной науки.
Эти трудности обусловлены колоссальной многофакторностью процесса. Итоговые эксплуатационные характеристики синтезированного изделия являются сложной функцией множества технологических параметров. Физические явления, протекающие в микроскопической зоне взаимодействия лазера с металлическим порошком, включают в себя процессы стремительного плавления, интенсивного кипения, сложного тепло- и массопереноса, а также кристаллизации в экстремально неравновесных условиях. Именно поэтому применение методов компьютерного моделирования является наиболее целесообразным и экономически оправданным подходом для исследования влияния всего комплекса теплофизических, физико-химических и технологических параметров на качество и надежность получаемых деталей.
1. Теоретические основы и ключевые физические процессы СЛП
Многообразие и взаимосвязь физических явлений (Рис. 1), протекающих в ванне расплава во время селективного лазерного плавления, напрямую определяют стабильность всего технологического процесса. Глубокое выявление и понимание этих явлений, а также их синергетического взаимодействия, имеет решающее значение для получения качественных изделий с воспроизводимыми свойствами.
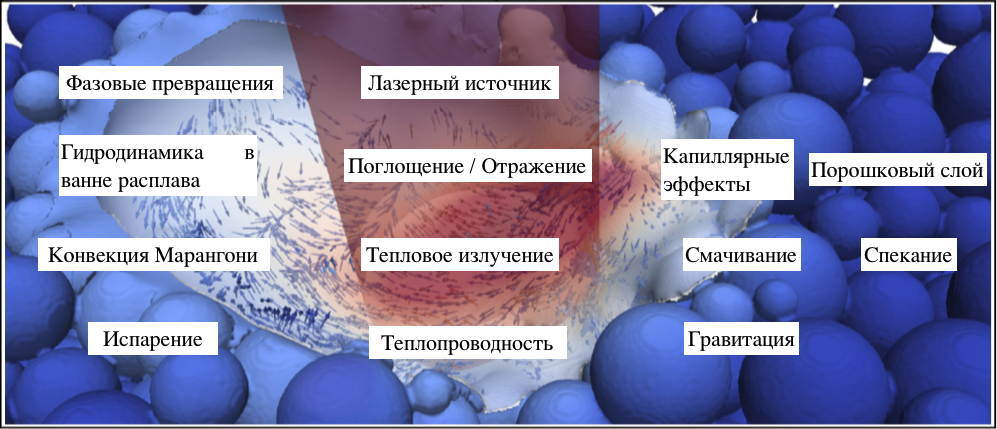
Рис. 1. Процессы, происходящие в ванне расплава при селективном лазерном или электронно-лучевом плавлении
1.1. Взаимодействие лазерного излучения с порошковым слоем
На начальном этапе лазерный луч облучает слой порошка. В отличие от сплошного материала, порошковая среда обладает уникальными оптическими свойствами. Из-за многократного переотражения от поверхностей отдельных частиц, лазерное излучение проникает на значительную глубину засыпки. Этот эффект приводит к объемному, а не поверхностному, характеру первоначального нагрева, что является фундаментальной особенностью процесса.
Теплофизические параметры порошковой композиции, такие как эффективная теплопроводность, определяют скорость и характер переноса тепла от формирующейся ванны расплава вглубь материала. Не менее важную роль играют и оптические свойства, в частности, поглощательная способность порошка. Именно они диктуют, какая доля энергии лазера будет усвоена материалом, а какая — отражена, что напрямую влияет на всю тепловую картину процесса.
1.2. Влияние характеристик порошка на качество синтеза
Качество исходного порошкового материала является краеугольным камнем успешного СЛП-процесса. Ключевые параметры порошков, включая их химический состав, гранулометрическое распределение и морфологию частиц, строго регламентируются стандартами, например, ГОСТ Р 57910-2017 «Аддитивные технологии. Металлические порошки. Общие требования».
В исследованиях было убедительно показано критическое влияние формы частиц на плотность засыпки. Чем ближе форма частиц к идеальной сфере, тем выше достигаемая насыпная плотность. Частицы неправильной, менее сферичной формы склонны к образованию агломератов и мостиковых структур, что приводит к появлению крупных протяженных пор в слое. Такие поры могут сохраняться в готовом изделии, становясь концентраторами напряжений и снижая его прочность.
Анализ влияния размера частиц на свойства конечных изделий выявил важную закономерность: для получения плотных, беспористых структур необходимо наличие мелкодисперсной фракции. При лазерном воздействии именно мелкие частицы плавятся в первую очередь, создавая жидкую фазу, которая смачивает более крупные частицы и способствует их эффективному плавлению, формируя гомогенную ванну расплава.
В одной из работ было детально исследовано влияние добавок малых частиц. Установлено, что введение около 15% частиц меньшего диаметра позволяет достичь максимальной теплопроводности порошкового слоя за счет заполнения межчастичных пустот. Одновременно с этим увеличивается и плотность засыпки, что в процессе сплавления минимизирует усадку и способствует значительному уменьшению остаточной пористости в готовых деталях.
1.3. Динамика ванны расплава: сложный мир гидродинамики
При достижении температуры солидуса сплава начинается формирование ванны расплава — микроскопического «реактора», где и происходят основные превращения. Несмотря на крайне малое время жизни (миллисекунды), поведение расплава претерпевает существенные изменения под действием целого комплекса сил.
В процессе нагрева действуют классические механизмы теплопереноса: конвекция, теплопроводность и излучение, которые определяют тепловые потери из зоны плавления. Величина конвективной теплоотдачи зависит от состава защитного газа в рабочей камере (обычно аргон или азот) и наличия системы принудительного обдува.
Интенсивность конвективных потоков внутри самой ванны расплава определяется вязкостью жидкого металла и силами, приводящими его в движение. Ключевыми из них являются:
- Термокапиллярная конвекция (эффект Марангони): Это движение жидкости, вызванное градиентом поверхностного натяжения. В центре ванны расплава, где температура максимальна, поверхностное натяжение ниже, а у более холодных краев — выше. Этот перепад заставляет жидкость течь от центра к периферии, что интенсифицирует теплообмен и влияет на геометрию ванны.
- Давление отдачи паров: При высоких плотностях энергии лазера происходит интенсивное испарение металла. Образующиеся пары создают реактивное давление на поверхность расплава, выталкивая жидкость и формируя глубокую парогазовую полость, известную как «keyhole». Этот режим может привести к образованию специфической «замочной скважины», но его нестабильность часто становится причиной образования газовых пор (keyhole-пористость).
- Капиллярные силы и смачиваемость: Высокое поверхностное натяжение и хорошая смачиваемость обеспечивают формирование гладкой и стабильной ванны расплава, что критически важно для образования сплошного трека.
Нарушение стабильности ванны расплава, особенно при высоких скоростях сканирования, может привести к ее распаду на отдельные капли вместо формирования сплошного валика. Этот эффект, известный как нестабильность Рэлея-Плато, является одной из основных причин образования дефектов несплавления и повышенной шероховатости поверхности.
1.4. Формирование единичных треков и их морфология
Для разработки качественной модели и подбора оптимальных параметров необходимо глубокое понимание процессов формирования отдельных лазерных треков. Условия их образования можно разделить на две фундаментальные группы:
- Формирование трека в слое порошка без влияния сплошной подложки (характерно для внутренних областей детали).
- Формирование трека на поверхности сплошной подложки или ранее сплавленного слоя.
В одной из знаковых работ описываются эксперименты по созданию одиночных треков на поверхности порошка для трех марок сталей. Результаты были сведены в номограмму (Рис. 2), показывающую зависимость конфигурации трека от скорости сканирования и мощности лазера. На диаграмме четко прослеживаются несколько областей с характерной морфологией треков.
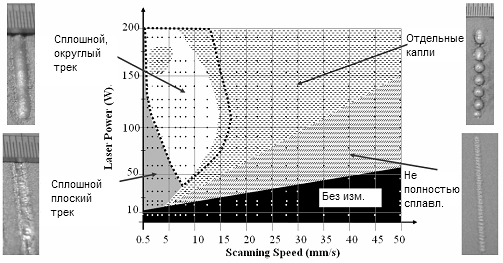
Рис. 2. Конфигурация трека при различных скоростях движения лазера и мощности для стали 314S
В области низких мощностей и скоростей (нижний левый угол) происходит лишь частичное проплавление порошка. Выход захваченных газов и усадка приводят к образованию вогнутого, нестабильного трека. С ростом мощности и скорости трек приобретает стабильную цилиндрическую форму, а его масса увеличивается.
При дальнейшем увеличении скорости сканирования гидродинамическая нестабильность жидкой фазы нарастает. Это приводит сначала к появлению разрывов в треке (balling effect), а затем и к его полному распаду на отдельные капли под действием уже упомянутой нестабильности Рэлея-Плато (Рис. 4).
Наконец, при очень высоких скоростях или недостаточной мощности, подводимой энергии не хватает для достижения температуры ликвидуса, и вместо плавления происходит лишь спекание отдельных частиц, либо процесс не инициируется вовсе.
1.5. Взаимодействие трека с подложкой
Немаловажным аспектом является сплавление трека на поверхности сплошной подложки, будь то стартовая плита построения или предыдущие слои. Здесь в игру вступают процессы теплоотвода в массивный объем, припекание трека и глубина проплавления подложки, которая обеспечивает металлургическую связь между слоями.
Эксперименты по оплавлению подложки без порошка показали линейную зависимость ширины и глубины проплавления от вложенной энергии. С увеличением скорости сканирования влияние теплопроводности подложки ослабевает, и ширина трека приближается к диаметру лазерного пятна.
При исследовании спекания трека из порошка нержавеющей стали 904L на подложке из стали 304L (при толщине слоя 50 мкм) была выявлена так называемая область консолидации порошка. Это зона вокруг расплавленного валика, где порошок спекается и «прилипает» к подложке, но не образует сплошного металла. Этот эффект необходимо учитывать при расчете шага штриховки (расстояния между соседними треками), чтобы избежать дефектов несплавления (Рис. 3).
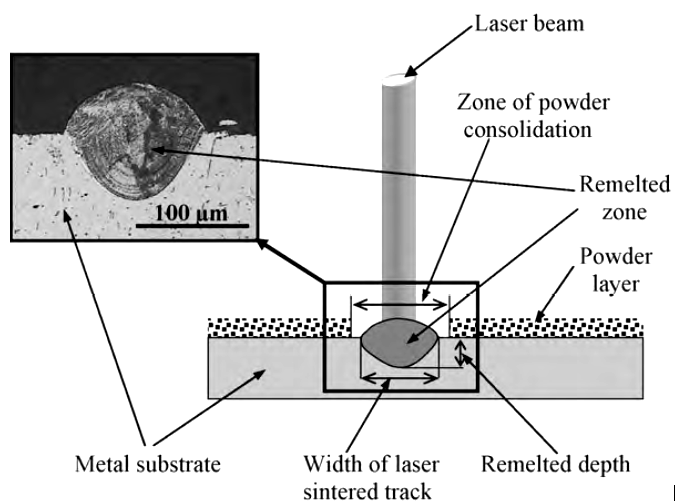
Рис. 3. Схема консолидации порошка в процессе СЛП
Исследования также показали, что при низких скоростях и малых мощностях теплоотвод в подложку настолько мал, что ванна расплава перегревается, что парадоксальным образом также ведет к нестабильности и разрыву трека.

Рис. 4. Изображение треков, искаженных за счет действия капиллярной нестабильности Рэлея-Плато
1.6. Фазовые превращения и микроструктура
Описание фазовых превращений — это, пожалуй, самая значимая и сложная часть моделирования СЛП. В отличие от спекания (SLS), где частицы лишь соединяются в точках контакта, при СЛП происходит их полное расплавление с образованием жидкой фазы. Процессы плавления и последующей кристаллизации протекают с колоссальными скоростями (скорости охлаждения могут достигать 105-107 К/с), что делает их глубоко неравновесными.
В результате такой сверхбыстрой кристаллизации формируется уникальная мелкозернистая, часто столбчатая микроструктура с метастабильными фазами, которая и определяет высокие механические свойства СЛП-изделий. Для предсказания этих свойств необходимо точное моделирование фазовых превращений. При экстремальных скоростях охлаждения может даже нарушаться принцип локального равновесия, приводя к бездиффузионной кристаллизации, когда твердая фаза наследует химический состав жидкой.
С увеличением мощности лазера глубина проплавления подложки растет (Рис. 5), что улучшает межслоевое сцепление. Одновременно изменяется и угол смачивания расплавом подложки (Рис. 6). При низкой мощности смачиваемость плохая (большой угол), что мешает формированию качественного слоя. С ростом мощности текучесть расплава увеличивается, угол смачивания уменьшается, что является благоприятным фактором для процесса СЛП.
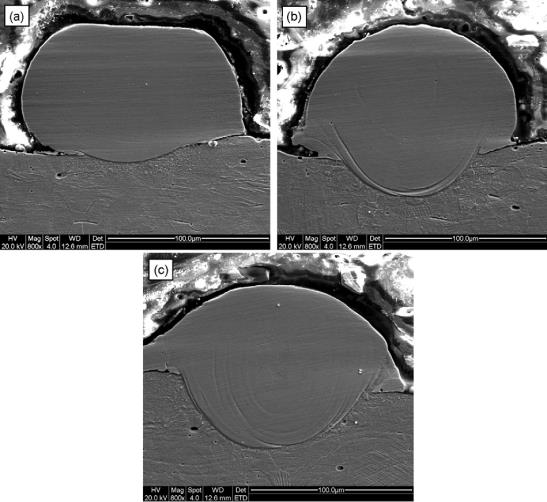
Рис. 5. Сечения треков, полученных при различных мощностях лазерного излучения: (a) – 60 Вт; (b) – 80 Вт; (c) – 100 Вт. Скорость лазерного луча постоянная.

Рис. 6. Сечения треков, полученных при различных скоростях сканирования: (a) – 150 мм/с; (b) – 60 мм/с; (c) – 20 мм/с. Мощность лазера – 100 Вт – постоянная.
2. Подходы к моделированию процесса селективного лазерного плавления
В научном сообществе не существует единого, универсального подхода к моделированию СЛП. Выбор метода определяется целями исследования: от анализа гидродинамики одиночной ванны расплава до прогнозирования остаточных напряжений в крупногабаритной детали. В Таблице 1 представлен обзор основных численных методов и их типичной области применения.
Таблица 1. Численные модели и их применимость в аддитивном производстве
| Метод моделирования | Область применения |
| Метод дискретных элементов (DEM) | Моделирование укладки и плотности порошкового слоя |
| Метод Монте-Карло (трассировка лучей) | Расчет поглощения лазерного излучения порошком |
| Метод решеточных уравнений Больцмана (LBM) | Детальный анализ гидродинамики и тепломассопереноса |
| Метод конечных объемов (FVM) | Анализ течения расплава и термодинамических полей |
| Метод конечных элементов (FEM) | Термомеханический анализ, расчет напряжений и деформаций |
| Метод конечных разностей (FDM) | Решение задач теплопроводности |
| Метод фазового поля (PFM) | Прогнозирование и эволюция микроструктуры |
| Метод клеточных автоматов (CA) | Моделирование роста и эволюции зеренной структуры |
Глобально все подходы можно разделить на два основных класса.
2.1. Микромасштабное моделирование: подход с явным разрешением частиц
Первый подход предполагает задание точной геометрии для каждой отдельной частицы порошка с учетом их реальной конфигурации. В таких моделях одновременно решаются задачи термодинамики и гидродинамики, что позволяет детально изучить такие явления, как плавление частиц, слияние капель, формирование мениска и капиллярные эффекты (Рис. 7).
Однако этот подход чрезвычайно требователен к вычислительным ресурсам. Учитывая малый размер частиц (5-50 мкм), требуется очень мелкая расчетная сетка. Согласно критерию устойчивости Куранта-Фридрихса-Леви, это накладывает жесточайшие ограничения на шаг по времени, который может составлять единицы наносекунд. Поэтому данный метод применим лишь для исследования микроскопических объемов системы (в пределах одного трека) и коротких промежутков времени.
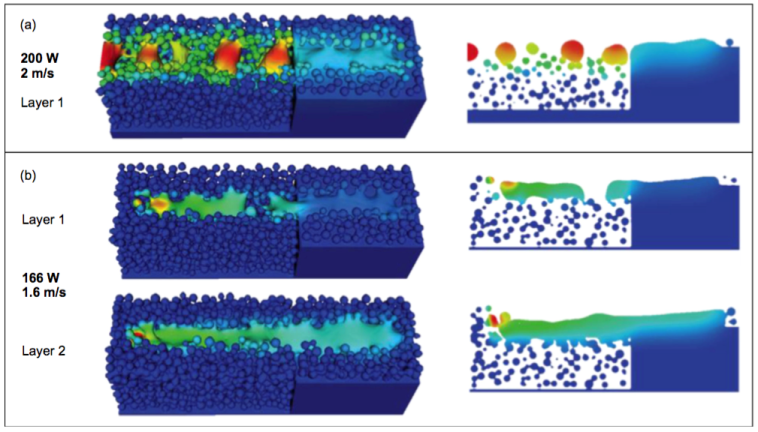
Рис. 7. Моделирование образования сплошной твёрдой фазы после единичного лазерного прохода с явным учетом частиц
2.2. Макро- и мезомасштабное моделирование: метод гомогенизированной среды
Более распространенным является подход, использующий модель сплошной (гомогенизированной) среды. В этом случае исследуемая система представляется как континуум, без явного разделения на частицы (Рис. 8). Свойства порошкового слоя (теплопроводность, плотность, поглощательная способность) задаются как эффективные, усредненные значения.
Такой подход не позволяет детально учесть поверхностные эффекты на уровне отдельных частиц, но зато он значительно экономит вычислительные ресурсы, позволяя моделировать построение целых слоев и даже небольших деталей.
Основным уравнением в данном случае является уравнение теплопроводности Фурье:
cρ(∂T/∂τ) = ∇(λ∇T) + Q(φs, T)
где T – температура; τ – время; c, ρ, λ – удельная теплоёмкость, плотность и теплопроводность материала; Q – функция объёмного источника тепла, учитывающая скрытую теплоту фазовых превращений (L). Q принимает отрицательное значение при плавлении и положительное при кристаллизации, завися от объёмной доли твёрдой фазы φs.
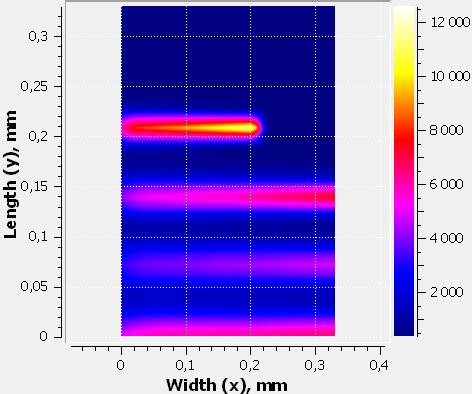
Рис. 8. Результаты моделирования теплового поля в процессе СЛП методом сплошной среды
Для описания поглощения лазерного излучения порошком часто используется закон Бугера-Ламберта-Бера:
I(z) = I0(1-R) · exp(-βz)
где I(z) – интенсивность излучения на глубине z; I0 – интенсивность на поверхности; R — коэффициент отражения; β – эффективный коэффициент поглощения. Недостаток модели в том, что коэффициент β является эмпирическим и требует подбора для каждого материала.
Более сложные модели, как предложенная Гусаровым, учитывают параметры засыпки (диаметр частиц, пористость) и многократные переотражения. Альтернативой является метод трассировки лучей, где моделируется путь каждого луча в хаотическом нагромождении частиц, что дает высокую точность, но требует огромных вычислений (Рис. 9).
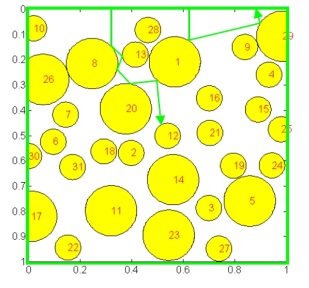
Рис. 9. Схема расположения частиц в модели трассировки лучей
2.3. Моделирование микроструктуры и остаточных напряжений
Финальная микроструктура изделия (дендритная, ячеистая или с плоским фронтом кристаллизации) определяется двумя ключевыми параметрами: градиентом температуры (G) на фронте кристаллизации и скоростью этого фронта (R). Соотношение G/R определяет морфологию, а произведение G×R — скорость охлаждения, которая влияет на размер структурных элементов (например, расстояние между ветвями дендритов). Диаграммы, подобные представленной на Рис. 10, позволяют прогнозировать тип формирующейся структуры в зависимости от локальных тепловых условий.
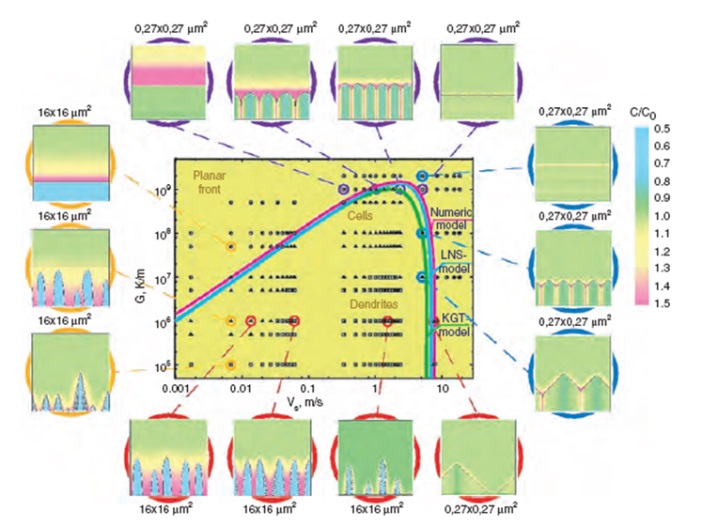
Рис. 10. Карта образования различных микроструктур в зависимости от градиента температур и скорости движения фронта кристаллизации
Для прогнозирования эволюции зеренной структуры часто используют гибридные подходы, комбинируя макроскопический расчет тепловых полей (FEM) с мезоскопическими моделями, такими как клеточные автоматы (CA), которые имитируют зарождение и рост зерен (Рис. 11).
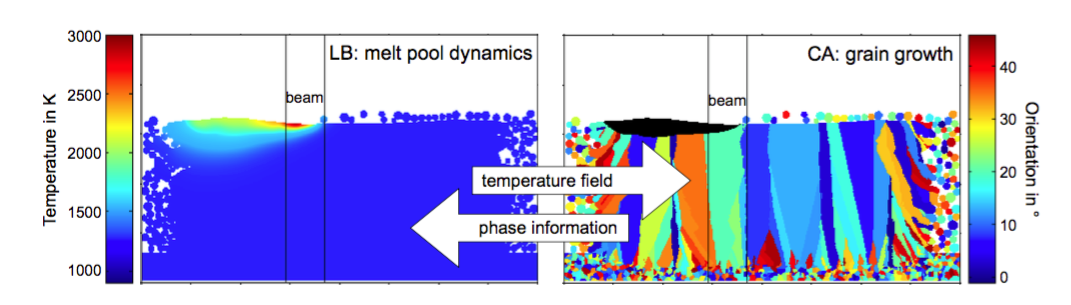
Рис. 11. Схема комбинации моделей массо- и теплопереноса (FEM) и фазообразования (CA) при моделировании
Одной из самых серьезных проблем аддитивного производства является возникновение остаточных напряжений. Из-за огромных и локализованных температурных градиентов различные участки детали расширяются и сжимаются неравномерно. Это приводит к накоплению внутренних напряжений, которые могут вызвать коробление детали после ее отделения от платформы (Рис. 12) или даже растрескивание в процессе построения.
Моделирование термомеханических процессов чрезвычайно сложно, поэтому часто расчеты ограничиваются несколькими слоями. Однако именно эти модели позволили разработать эффективные стратегии сканирования, такие как «островковая» или «шахматная», где слой разбивается на небольшие сегменты, которые сканируются в определенной последовательности. Это позволяет более равномерно распределить тепло и значительно снизить уровень остаточных напряжений.
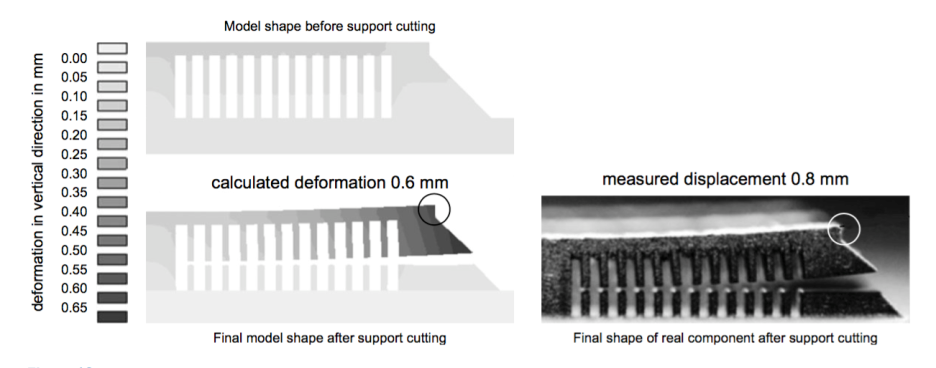
Рис. 12. Сопоставление результатов моделирования коробления с экспериментальным результатом
Заключение: Синергия моделирования и мониторинга в реальном времени
Компьютерное моделирование процессов селективного лазерного плавления прошло долгий путь от простых тепловых моделей до сложных мультифизических симуляций, способных предсказывать микроструктуру и механические свойства изделий. Понимание физических явлений на всех уровнях — от поведения отдельных частиц порошка до накопления напряжений в готовой детали — позволяет инженерам и исследователям целенаправленно управлять процессом и предотвращать возникновение дефектов.
Следующим революционным шагом в развитии аддитивных технологий станет синергия предиктивного моделирования и систем мониторинга в реальном времени (in-situ monitoring). Оборудование, оснащенное пирометрами, тепловизорами и высокоскоростными камерами, собирает огромный массив данных о состоянии ванны расплава в каждый момент времени (Рис. 13).

Рис. 13. Сопоставление результатов рентгеновской томографии образца (1) и данных с системы мониторинга (2), указывающих на аномальные зоны
Будущее за интеграцией этих данных с быстрыми («суррогатными») моделями на основе машинного обучения. Такие системы смогут не просто предсказывать возможные дефекты, но и активно предотвращать их появление, корректируя параметры лазера «на лету». Это ознаменует переход от простого производства к интеллектуальному «выращиванию» изделий с гарантированным качеством, открывая новую эру в цифровом производстве.
