Содержание страницы
- 1. Базовые Термины и Определения в Механике
- 2. Классификация Звеньев Механизма
- 3. Классификация Кинематических Пар (КП)
- 4. Типовые Подвижные Звенья и их Назначение
- 5. Кинематические Цепи: Структура и Типы
- 6. Обзор Основных Видов Механизмов
- 7. Структурный Анализ Плоских Механизмов
- 8. Замена Высших Кинематических Пар Низшими
- Заключение: Роль ТММ в Современной Инженерии
С древнейших времен человечество стремилось облегчить свой труд и расширить физические возможности. От простого рычага, описанного Архимедом, до сложных паровых машин, давших толчок промышленной революции, в основе прогресса всегда лежало гениальное искусство создания устройств, способных преобразовывать движение и энергию. Именно это искусство легло в основу фундаментальной инженерной дисциплины — Теории механизмов и машин (ТММ). Эта наука является своего рода «грамматикой» для любого инженера-механика, предоставляя инструменты для анализа существующих и синтеза новых, более совершенных конструкций.
В этой статье мы совершим глубокое погружение в мир ТММ. Мы начнем с базовых определений — что такое машина, механизм, звено и кинематическая пара, — и постепенно перейдем к более сложным темам, таким как структурный анализ и классификация механизмов по методу выдающегося ученого Л. В. Ассура. Материал предназначен не только для студентов технических вузов, но и для всех, кто хочет понять, как на самом деле «работает» мир механики, от двигателя вашего автомобиля до сложнейших промышленных роботов.
1. Базовые Термины и Определения в Механике
Машина – это созданное человеком техническое устройство, которое выполняет целенаправленные механические движения с целью преобразования энергии, обработки материалов или передачи информации. Ключевой и неотъемлемый признак любой машины — совершение полезной работы, направленной на облегчение или полную замену физического и умственного труда человека.
Всё многообразие существующих машин принято классифицировать на четыре глобальные категории.
1. Энергетические машины – это устройства, чья основная функция заключается в преобразовании энергии одного вида в другой. Они являются сердцем современной энергетики и промышленности.
- Двигатели – энергетические машины, трансформирующие любой вид энергии (электрическую, тепловую, химическую) в механическую работу. Примерами служат электродвигатели, преобразующие электроэнергию в вращение вала, или двигатели внутреннего сгорания (ДВС), где энергия расширяющихся газов от сгорания топлива толкает поршни.
- Генераторы – энергетические машины, выполняющие обратную задачу: они преобразуют механическую энергию в энергию иного вида, чаще всего в электрическую. Классический пример — электрогенератор на гидроэлектростанции, который превращает механическую энергию вращения турбины под действием потока воды в электрический ток.
2. Рабочие машины – это наиболее обширный класс машин, которые используют подведенную к ним энергию для выполнения конкретной технологической или транспортной функции, изменяя объект труда.
- Транспортные машины – предназначены для перемещения грузов, людей или материалов в пространстве. К ним относятся автомобили, конвейерные ленты, самолеты, лифты и суда.
- Технологические машины – целенаправленно изменяют форму, размеры, свойства или состояние обрабатываемого объекта. Это станочный парк (токарные, фрезерные станки), прессы, компрессоры, ткацкие станки и строительная техника.
3. Информационные машины – устройства, созданные для преобразования, хранения и обработки информации, представленной в виде данных. Это основа цифровой эры, от персональных компьютеров и серверов до калькуляторов и смартфонов.
4. Кибернетические машины – представляют собой высший уровень развития техники, объединяя в себе признаки других видов машин и обладая продвинутыми системами управления, часто с элементами искусственного интеллекта. Они способны управлять другими машинами или автономно выполнять сложные задачи. Яркие представители этого класса — промышленные роботы-манипуляторы на сборочных линиях, беспилотные летательные аппараты (дроны) и автоматизированные комплексы.
В отличие от машины, Механизм – это система соединенных между собой тел (звеньев), спроектированная для преобразования движения одного или нескольких тел в требуемое, заранее определенное движение других тел. Важнейшее отличие заключается в том, что механизм сам по себе не совершает полезной работы, а лишь обеспечивает необходимую кинематику — закон движения своих звеньев.
Любой механизм должен строго соответствовать требованиям, изложенным в техническом задании на его проектирование. Качество его структуры оценивается по комплексу критериев: конструктивная простота, технологичность изготовления звеньев, экономичность, надежность в эксплуатации, долговечность, а также массогабаритные показатели.
Основой любого механизма являются его составляющие части.
Звено механизма – это деталь или совокупность нескольких жестко соединенных между собой деталей, которые в рамках механизма движутся как единое целое.
Все неподвижные детали механизма, служащие его основанием (например, корпус редуктора, станина станка), условно объединяются в одно неподвижное звено, именуемое стойкой.
Звенья в механизме соединены таким образом, что всегда обеспечивается их взаимное относительное движение.
Подвижное соединение двух соприкасающихся звеньев называется кинематической парой (КП). Именно через кинематические пары реализуется передача движения и сил.
Те части звена (поверхности, линии или точки), по которым оно контактирует с другим звеном, формируя кинематическую пару, называются элементами звена.
Система звеньев, последовательно соединенных кинематическими парами, образует кинематическую цепь. Таким образом, любой механизм представляет собой кинематическую цепь, в которой одно из звеньев является неподвижной стойкой.
Изучение и проектирование механизмов и машин ведется с использованием их упрощенных образов — моделей. В соответствии с ГОСТ 2.770-68 «ЕСКД. Обозначения условные графические на схемах. Элементы кинематики», для представления механизмов используются стандартизированные схемы.
Модель – это упрощенный образ реального объекта или процесса, который адекватно отражает его ключевые свойства, необходимые для исследования. Моделирование позволяет анализировать и оптимизировать конструкцию еще до ее физического воплощения.
Модели механизмов классифицируются по различным признакам:
- По форме представления: физические (макеты) и математические (системы уравнений).
- По методу анализа: графические, аналитические (численные), графоаналитические, динамические и др.
При создании модели вводятся определенные допущения, которые упрощают расчеты:
- Все звенья считаются абсолютно твердыми и жесткими, то есть их деформации под нагрузкой пренебрежимо малы.
- Контактирующие поверхности звеньев являются идеально гладкими, что позволяет на начальных этапах анализа не учитывать силы трения.
- Механизмы рассматриваются исключительно как преобразователи движения и сил, без учета реальных условий эксплуатации (температура, влажность и т.д.).
Эти допущения значительно упрощают анализ и синтез на ранних стадиях проектирования. В зависимости от требуемой точности расчетов, количество допущений может быть уменьшено. Наиболее наглядной моделью является схема, которая может быть функциональной, структурной, кинематической или динамической.
2. Классификация Звеньев Механизма
Независимо от сложности конструкции, любая машина или механизм состоит из ограниченного набора базовых элементов: звеньев и кинематических пар.
По конструктивному исполнению звенья делятся на простые и сложные.
Простое звено – это звено, которое входит в состав не более чем двух кинематических пар. На схемах его можно представить в виде отрезка прямой, соединяющего центры этих пар (рис. 1). Примерами служат стержни, ползуны, а также зубчатые колеса и кулачки, которые соединяются с другими звеньями.
На кинематических схемах простые звенья условно изображаются в виде линий или кривых.
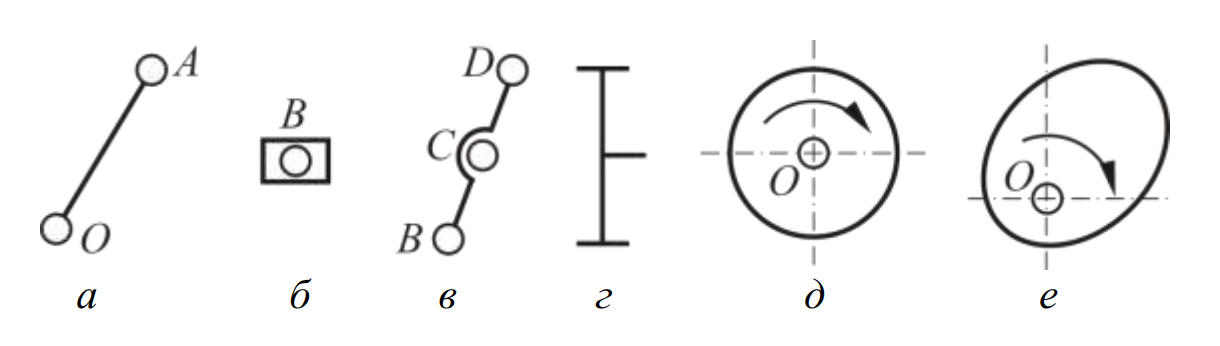
Рисунок 1 – Простые звенья
Сложное (составное) звено – это звено, входящее в состав трех и более кинематических пар. Через центры этих пар можно провести более одной прямой (рис. 2).
Сложные звенья на схемах изображаются в виде геометрических фигур (треугольников, многоугольников), которые для наглядности заштриховываются.
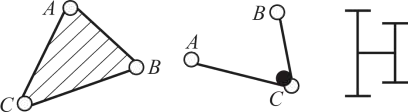
Рисунок 2 – Сложные звенья
Сложные звенья вводятся в конструкцию для повышения жесткости или для реализации более сложных траекторий движения. Однако, с точки зрения структурного анализа, более важной является классификация по числу элементов (вершин), которыми звено присоединяется к другим.
По кинематическому состоянию звенья делятся на подвижные и неподвижные относительно выбранной системы отсчета. Неподвижное звено, как уже упоминалось, называется стойкой.
На схемах все неподвижные элементы (опоры, направляющие) относятся к стойке, которая обозначается символом «0» и помечается штриховкой под углом 45°. Стойка всегда одна, но может быть изображена в разных частях схемы для удобства. Подвижные звенья нумеруются арабскими цифрами (рис. 3).
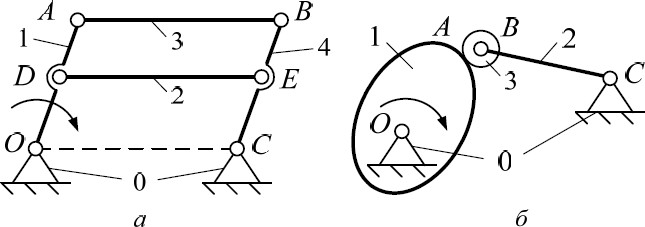
Рисунок 3 – Схемы механизмов с нумерацией звеньев
По функциональному назначению в процессе преобразования движения звенья классифицируются следующим образом:
- Ведущее (входное) звено – это звено, которому сообщается движение от внешнего источника энергии (двигателя). Оно приводит в движение весь механизм. На разных этапах работы ведущим может становиться разное звено. В ДВС на такте рабочего хода поршень является ведущим, а на остальных тактах ведущим становится кривошип, вращаемый маховиком.
- Ведомое (выходное) звено – звено, которое совершает требуемое технологическое движение, ради которого механизм и был создан. Оно связано с рабочим органом машины.
- Соединительное (промежуточное) звено – все остальные звенья, передающие движение от ведущего к ведомому звену.
Механизмы могут иметь сложную структуру входов и выходов:
- Дифференциальные механизмы имеют одно входное звено и несколько выходных, движение которых зависит друг от друга (например, автомобильный дифференциал, распределяющий крутящий момент между колесами).
- Суммирующие механизмы имеют несколько входных звеньев и одно выходное, движение которого является суммой движений входных.
Начальным звеном при анализе называют звено, от которого наиболее удобно начинать расчет кинематических параметров всего механизма. Оно не обязательно совпадает с ведущим звеном.
3. Классификация Кинематических Пар (КП)
Кинематическая пара, как подвижное соединение двух звеньев, является ключевым элементом любого механизма. Ее характеристики определяют характер относительного движения и долговечность узла.
По виду контакта между элементами звеньев различают:
- Высшие КП, в которых контакт происходит по линии или в точке (рис. 4, а). Примеры: кулачок и толкатель, зацепление зубьев колес.
- Низшие КП, в которых контакт осуществляется по поверхности. Примеры: шарнир (вращательная пара), ползун в направляющих (поступательная пара).
Низшие пары обладают большей износостойкостью и несущей способностью, так как нагрузка распределяется по большей площади, создавая меньшее удельное давление. Поэтому в силовых механизмах предпочтение отдается низшим КП. Однако высшие КП позволяют создавать более компактные механизмы для реализации сложных законов движения.
По способу обеспечения контакта (замыкания) звеньев:
- Силовое замыкание – постоянный контакт обеспечивается внешней силой, например, силой тяжести или упругостью пружины (рис. 4, а).
- Геометрическое замыкание – контакт обеспечивается самой конструкцией (геометрией) сопрягаемых элементов (рис. 4, б).
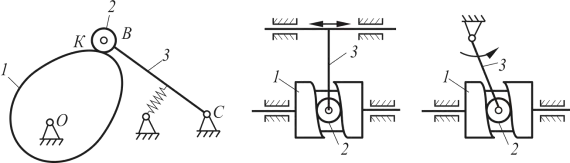
Рисунок 4 – Способы замыкания в кинематических парах
Свободное твердое тело в пространстве обладает шестью степенями свободы: три независимых поступательных движения вдоль осей X, Y, Z и три вращательных движения вокруг этих же осей (рис. 5).
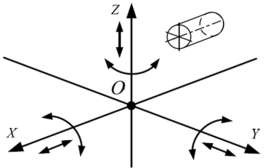
Рисунок 5 – Возможные перемещения механической системы
Когда звено входит в кинематическую пару, на его относительное движение накладываются ограничения, называемые условиями связи. Каждое условие связи отнимает одну степень свободы.
По числу наложенных условий связи (S) КП подразделяют на пять классов. Класс пары определяется количеством связей S, а ее подвижность (число оставшихся степеней свободы) вычисляется как H = 6 — S.
Таблица 1 – Классификация и виды кинематических пар
| Класс | Число связей, S | Подвижность, H | Пространственная схема | Вид контакта | Условное обозначение |
| Кинематическая пара «шар–плоскость» | |||||
| 1 | 1 | 5 (3 вращ. + 2 пост.) | 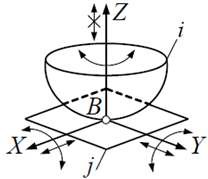 |
Точечный, высшая | 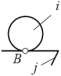 |
| Кинематическая пара «цилиндр–плоскость» | |||||
| 2 | 2 | 4 (2 вращ. + 2 пост.) | 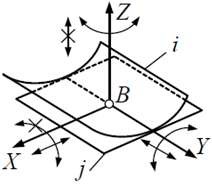 |
Линейный, высшая | 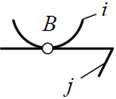 |
| Кинематическая пара «сферическая» (шаровой шарнир) | |||||
| 3 | 3 | 3 (3 вращ.) | 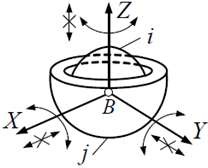 |
Поверхностный, низшая | 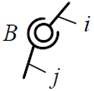 |
| Кинематическая пара «цилиндрическая» | |||||
| 4 | 4 | 2 (1 вращ. + 1 пост.) | 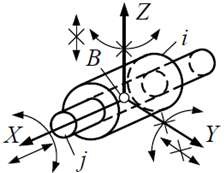 |
Поверхностный, низшая | 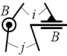 |
| Кинематическая пара «поступательная» | |||||
| 5 | 5 | 1 (1 пост.) | 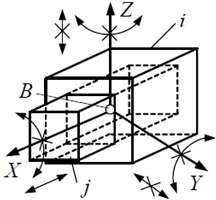 |
Поверхностный, низшая | 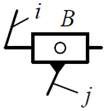 |
| Кинематическая пара «вращательная» | |||||
| 5 | 5 | 1 (1 вращ.) | 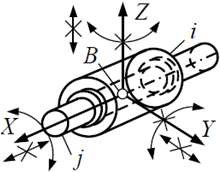 |
Поверхностный, низшая | 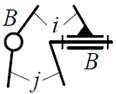 |
Примечание: в таблице «вращ.» обозначает вращательное движение, «пост.» – поступательное движение.
4. Типовые Подвижные Звенья и их Назначение
В зависимости от характера совершаемого движения и конструктивного исполнения, подвижные звенья имеют устоявшиеся названия, отражающие их функцию в механизме (рис. 6 и табл. 2).
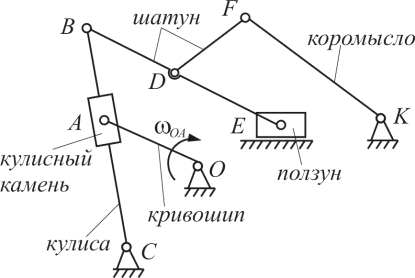
Рисунок 6 – Виды подвижных звеньев
Звенья, совершающие вращательное движение:
- Кривошип – звено, способное совершать полный оборот (на 360° и более) вокруг неподвижной оси.
- Коромысло – звено, совершающее неполноповоротное (качательное) движение вокруг неподвижной оси на угол менее 360°.
- Зубчатое (или фрикционное) колесо – звено, передающее вращательное движение другому звену посредством зацепления или сил трения.
Звенья, совершающие поступательное движение:
- Ползун – звено, движущееся прямолинейно в неподвижных направляющих.
- Толкатель – ведомое звено в кулачковом механизме, совершающее, как правило, возвратно-поступательное движение.
Звенья, совершающие сложное плоскопараллельное движение:
- Шатун – звено, которое не имеет непосредственной связи со стойкой и соединяет два других подвижных звена (например, кривошип и ползун).
- Кулиса – звено, одновременно участвующее во вращательном и поступательном движении, образуя направляющую для другого звена (кулисного камня).
Таблица 2 – Характеристики типовых подвижных звеньев
| Название звена | Условное обозначение | Тип движения | Ключевые особенности |
| 1. Кривошип |  |
Вращательное | Способен совершить полный оборот (угол > 360°) |
| 2. Шатун |  |
Плоскопараллельное | Соединяет только подвижные звенья, не связан со стойкой |
| 3. Коромысло |  |
Вращательное (качательное) | Угол поворота всегда меньше 360° |
| 4. Ползун | Поступательное | Движется в неподвижных направляющих (стойке) | |
| 5. Кулиса и кулисный камень |  |
Вращательное и сложное | Направляющая для камня сама является подвижным звеном |
| 6. Кулачок и толкатель | 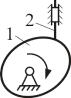 |
Вращательное и поступательное | Профиль кулачка определяет закон движения толкателя |
| 7. Колесо и рейка |  |
Вращательное и поступательное | Преобразуют вращение в поступательное движение и наоборот |
5. Кинематические Цепи: Структура и Типы
Как мы уже определили, совокупность звеньев, соединенных кинематическими парами, образует кинематическую цепь. Классификация цепей является основой для дальнейшего структурного анализа.
Кинематические цепи подразделяются:
- Простые, если каждое звено цепи входит не более чем в две КП (рис. 7, а).
- Сложные, если в цепи есть хотя бы одно звено, входящее в три и более КП (рис. 7, б).
- Замкнутые, если все звенья цепи входят как минимум в две КП, образуя замкнутый контур (рис. 7, а).
- Незамкнутые (открытые), если в цепи есть звенья, входящие только в одну КП (рис. 7, б).
- Плоские, если все точки звеньев движутся в параллельных плоскостях.
- Пространственные, если точки звеньев описывают пространственные кривые.
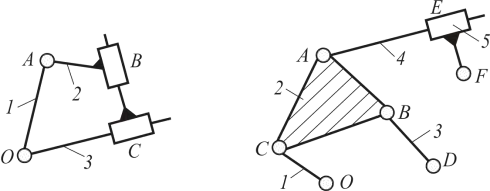
Рисунок 7 – Примеры простой (а) и сложной (б) кинематических цепей
Звенья, входящие лишь в одну КП в незамкнутой цепи, именуются поводками (на рис. 7, б, это звенья 1, 3, 5).
6. Обзор Основных Видов Механизмов
Механизм представляет собой кинематическую цепь, в которой одно звено зафиксировано (является стойкой), а движение выходных звеньев однозначно определяется движением входных.
Таблица 3 – Сравнительная таблица основных типов механизмов
| Тип механизма | Основной принцип | Преимущества | Недостатки | Типичные применения |
|---|---|---|---|---|
| Шарнирно-рычажные | Передача движения через звенья, соединенные низшими парами (шарнирами). | Высокая надежность, долговечность, простота, способность передавать большие усилия. | Сложность реализации точных траекторий, громоздкость. | ДВС, подвеска автомобиля, стеклоочистители, прессы. |
| Кулачковые | Ведомое звено движется по закону, заданному профилем ведущего звена (кулачка). | Простота реализации любого закона движения, компактность. | Высокие контактные напряжения, износ высшей пары, чувствительность к точности изготовления. | Газораспределительные механизмы ДВС, автоматы, станки. |
| Зубчатые | Передача вращения через зацепление зубьев. Соответствует ГОСТ 16530-83. | Постоянство передаточного отношения, высокий КПД, передача больших мощностей, компактность. | Шум при работе, необходимость точного изготовления и смазки. | Редукторы, коробки передач, часы, приводы станков. |
| Винтовые | Преобразование вращательного движения в поступательное с помощью пары «винт-гайка». | Большой выигрыш в силе, точность перемещения, свойство самоторможения. | Низкий КПД из-за высокого трения, малая скорость перемещения. | Домкраты, прессы, приводы подач в станках, измерительные приборы. |
| Фрикционные | Передача движения за счет сил трения между прижатыми друг к другу телами. | Плавность, бесшумность, возможность бесступенчатого регулирования (вариаторы). | Проскальзывание (непостоянство передаточного отношения), потребность в силах прижатия. | Вариаторы, лентопротяжные механизмы, приборостроение. |
Рассмотрим некоторые из этих и другие виды механизмов подробнее.
Шарнирно-рычажные механизмы
Это механизмы, состоящие только из низших кинематических пар (в основном вращательных и поступательных). Они являются основой для множества машин благодаря своей надежности и простоте.
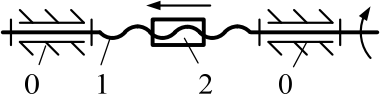
Рисунок 8 – Схема винтового механизма
Зубчатые механизмы
Предназначены для передачи вращательного движения с постоянным передаточным отношением. Если оси колес подвижны, механизм называют планетарным (рис. 9, б). Для передачи движения между перекрещивающимися осями используют червячную передачу (рис. 9, в).
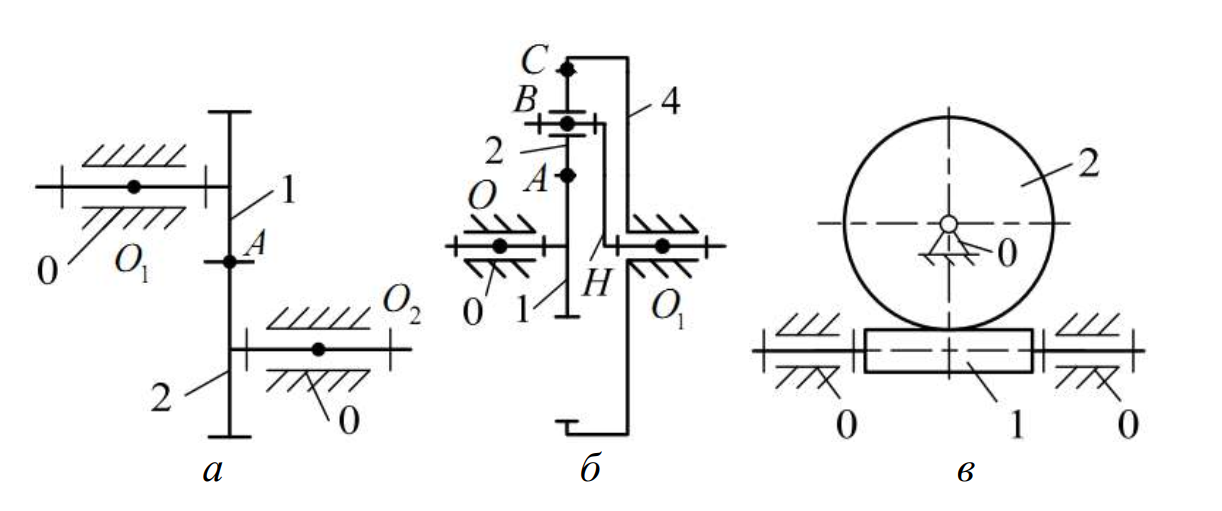
Рисунок 9 – Схемы зубчатых механизмов
Механизмы прерывистого движения
- Мальтийский механизм преобразует непрерывное вращение ведущего звена в прерывистое вращение ведомого, с четко выраженными остановками (рис. 10).
- Храповый механизм обеспечивает движение только в одном направлении, предотвращая обратный ход (рис. 11).
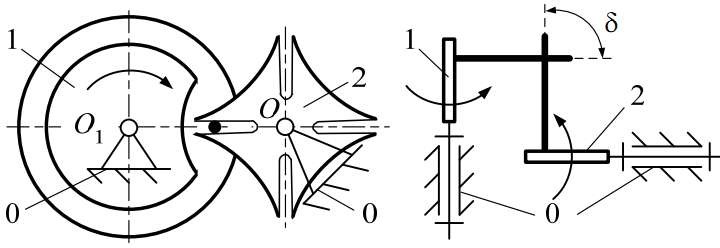
Рисунок 10 – Схемы мальтийских механизмов
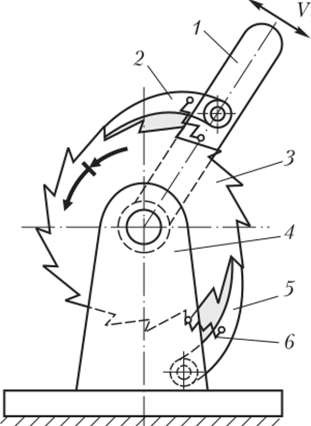
Рисунок 11 – Схема храпового механизма
Механизмы с гибкими звеньями
Для передачи движения на большие расстояния используются ременные, цепные или канатные передачи. Они позволяют соединять валы, расположенные на значительном удалении друг от друга.
Волновые механизмы
Принцип их действия основан на деформации гибкого звена (гибкого колеса) генератором волн (рис. 12). Это позволяет достигать огромных передаточных отношений в одной ступени, высокой кинематической точности и плавности хода.
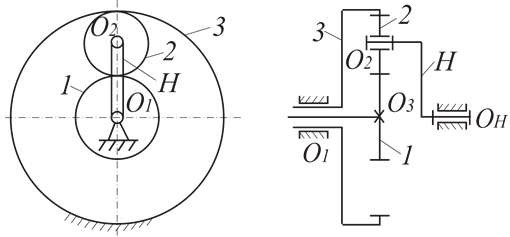
Рисунок 12 – Схема волнового механизма
7. Структурный Анализ Плоских Механизмов
Структурный анализ — это первый и важнейший этап исследования любого механизма. Его цель — определить состав механизма и то, как он образован из простейших структурных элементов.
Структурная схема – это графическое изображение механизма, выполненное по стандартам (например, ГОСТ 2.770-68) без соблюдения масштаба, но с точным отражением числа звеньев, вида и класса кинематических пар.
Ключевой характеристикой механизма является число степеней свободы (подвижность) W, которое показывает, скольким независимым параметрам нужно задать движение, чтобы положение всех звеньев системы было однозначно определено.
Для плоских механизмов, где каждое свободное звено имеет три степени свободы, подвижность определяется по формуле П. Л. Чебышева:
W = 3n − 2p5 − p4 (1)
где n – число подвижных звеньев, p5 – число низших пар 5-го класса (одноподвижных), p4 – число высших пар 4-го класса (двухподвижных).
Для пространственных механизмов используется формула Сомова-Малышева:
W = 6n − 5p5 − 4p4 − 3p3 − 2p2 − p1 (2)
Если W = 1, механизм имеет одно ведущее звено. Если W = 2 — два, и так далее.
Структурная классификация по Ассуру-Артоболевскому
Эта классификация позволяет разложить любой сложный механизм на простые составные части. Согласно ей, любой механизм состоит из первичного механизма и последовательно присоединенных к нему структурных групп (групп Ассура).
- Первичный механизм – это ведущее звено (или звенья), соединенное со стойкой. Он имеет ту же подвижность, что и весь механизм в целом (рис. 13).
- Группа Ассура – это кинематическая цепь с нулевой степенью подвижности (W=0), которая при присоединении к механизму не изменяет его общую подвижность. Проще говоря, это «жесткий» блок звеньев, который можно добавить к существующей конструкции.

Рисунок 13 – Первичные механизмы
Формула строения механизма показывает, как он «собран» из этих элементов:
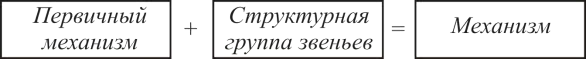
Рисунок 14 – Структура механизма по Ассуру
Группы Ассура классифицируются по классу (определяется числом КП в самом сложном контуре) и порядку (числом «внешних» элементов, которыми группа крепится к механизму).
Наиболее распространены двухповодковые группы Ассура II класса (рис. 15), состоящие из двух звеньев и трех кинематических пар.
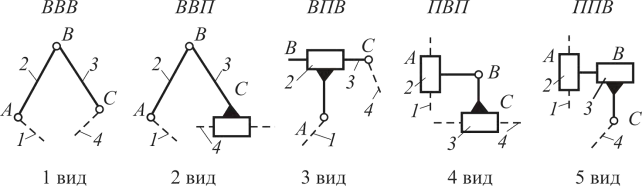
Рисунок 15 – Виды групп Ассура второго класса второго порядка
Класс механизма определяется наивысшим классом группы Ассура в его составе.
8. Замена Высших Кинематических Пар Низшими
Методы анализа механизмов с низшими парами разработаны лучше, поэтому часто при исследовании механизмов с высшими КП (зубчатых, кулачковых) их временно заменяют кинематически эквивалентными механизмами только с низшими парами. Эта замена справедлива только для конкретного мгновенного положения механизма.
Алгоритм замены:
- В точке контакта элементов высшей пары проводится общая нормаль.
- На этой нормали находятся центры кривизны контактирующих поверхностей.
- В эти центры помещаются новые вращательные шарниры, которые соединяются с исходными звеньями через новое «фиктивное» звено (рис. 16).
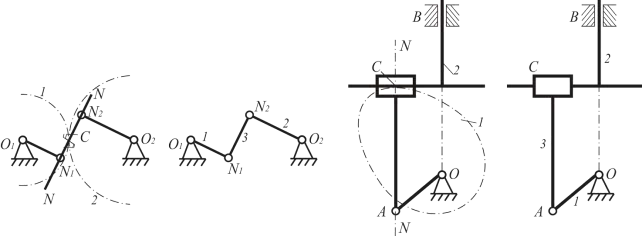
Рисунок 16 – Пример замены высшей КП на механизм с низшими КП
Подвижность исходного и заменяющего механизмов должна быть одинаковой. Например, для зубчатого механизма на рис. 16 (а) подвижность W = 3·2 – 2·2 – 1 = 1. Для заменяющего механизма W = 3·3 – 2·4 = 1. Подвижность сохранилась, замена корректна.
Порядок выполнения структурного анализа
- Начертить структурную схему механизма.
- При наличии высших пар, заменить их низшими.
- Определить степень подвижности (W) по формуле Чебышева.
- Выделить первичный механизм (ведущее звено и стойку).
- Последовательно, начиная с наиболее удаленных от ведущего звена, «снимать» с механизма группы Ассура, каждый раз проверяя, что подвижность оставшейся части не изменилась.
- Определить класс и порядок каждой выделенной группы.
- Записать итоговую формулу строения механизма.
Пример: Структурный анализ механизма грохота зерноуборочного комбайна (рис. 17).
Исходные данные: 5 подвижных звеньев (n=5), 7 низших пар (p5=7). Подвижность W = 3·5 – 2·7 = 1.
Вариант 1 (ведущее звено 1):
- Первичный механизм: (1, 0).
- Отделяем группу Ассура II класса, состоящую из звеньев 3 и 4.
- Отделяем следующую группу Ассура II класса, состоящую из звеньев 2 и 5.
- Остается первичный механизм.
Формула строения: I(1,0) → II(2,5) → II(3,4). Механизм второго класса.
Вариант 2 (ведущее звено 4):
- Первичный механизм: (4, 0).
- В этом случае невозможно выделить двухповодковые группы. Выделяется одна сложная трехповодковая группа III класса, состоящая из звеньев 1, 2, 3, 5.
Формула строения: I(4,0) → III(1,2,3,5). Механизм третьего класса.
Этот пример наглядно показывает, что класс механизма может зависеть от выбора ведущего звена.
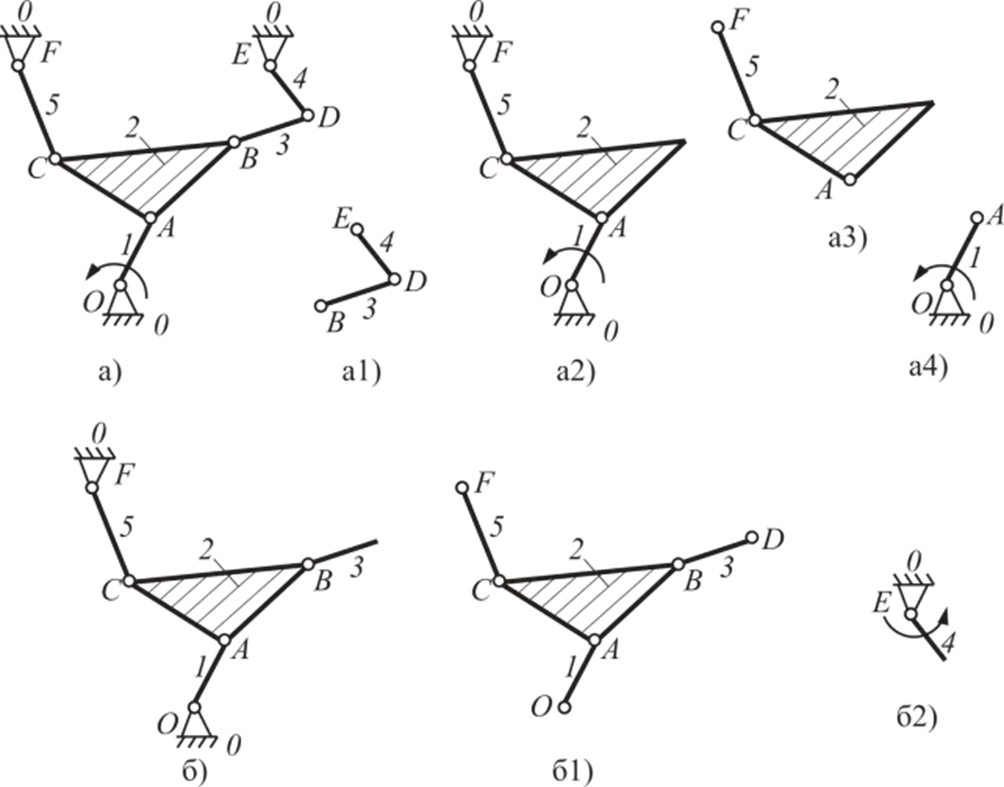
Рисунок 17 – Структурный анализ механизма грохота зерноуборочного комбайна
Заключение: Роль ТММ в Современной Инженерии
Теория механизмов и машин остается краеугольным камнем инженерного образования и практики. Рассмотренные нами принципы структурного анализа и классификации являются не просто академической теорией, а мощным практическим инструментом, позволяющим инженерам «читать» и понимать любые, даже самые сложные механические системы.
В современную эпоху развитие ТММ не останавливается. Появляются новые вызовы и направления:
- Мехатроника и робототехника: Интеграция классической механики с электроникой и компьютерным управлением требует комплексного подхода к проектированию.
- Компьютерное моделирование (CAD/CAE): Современные программные комплексы позволяют проводить кинематический и динамический анализ механизмов с высочайшей точностью еще на этапе проектирования, учитывая деформации звеньев и силы трения.
- Новые материалы: Применение композитов и аддитивных технологий (3D-печать) позволяет создавать звенья сложной формы с заданными свойствами, что расширяет возможности для синтеза новых механизмов.
Несмотря на появление новых технологий, фундаментальные законы и подходы, заложенные в ТММ, остаются неизменными. Понимание структуры, кинематики и динамики является ключом к созданию эффективных, надежных и инновационных машин, которые будут служить человечеству в будущем.
