Содержание страницы
Провод, закрепленный в двух точках на одинаковой высоте и испытывающий равномерно распределенную нагрузку от собственной массы, массы гололеда и давления ветра, можно рассматривать, как гибкую нить, принявшую форму цепной линии. При достаточно больших отношениях длины пролета L к стреле провеса f (что соответствует действительности) кривая провеса провода очень близка к параболе вида: ? = ℎ + ??2.
При совмещении начала координат с наинизшей точкой провеса линейного провода (рис. 1), (т.е. полагая h=0), уравнение параболы принимает вид: ? = ??2. Исходя из этого уравнения и, полагая длину провода в пролете примерно равной длине пролета (? ≈ ?), и с учетом силы тяжения Ti в каждой точке вдоль провода, обусловленной нагрузками на провод и зависящей от стрелы провеса провода, закрепленного между точками А и В получим формулу для расчета стрелы провеса провода.
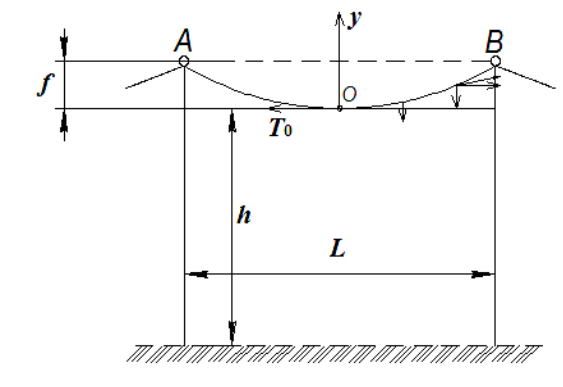
Рис. 1. Эскиз пролета воздушной линии электропередачи
Выделим участок ОС (рис. 1) с координатами О (0,0) и рассмотрим его равновесие. На отрезок провода в точках О и С действуют постоянные силы тяжения ТО и ТС, а также вертикальные нагрузки ??? = ?0?, где ?0– вертикальная нагрузка провода длиною 1м.
Условия равновесия отрезка будут соблюдены, если сумма проекций всех составляющих сил на оси х и у будет равна нулю, т.е.
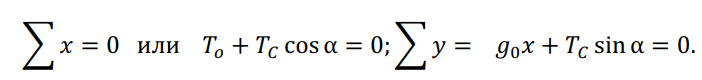
Тогда ![]() , а так как tg α характеризует угол наклона прямой в координатной плоскости x, y, т.е.
, а так как tg α характеризует угол наклона прямой в координатной плоскости x, y, т.е. ![]() , то получим
, то получим
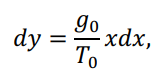
где ?0и T0 – постоянные величины, а y – текущая ордината кривой провеса провода:
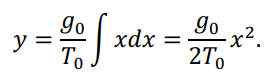
При ? = ?/2 (средина пролета) получим выражение для стрелы провеса провода для пролета
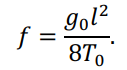
Выразив вертикальную нагрузку провода ?0 через его удельную нагрузку γ? = ?0/?, а также тяжение провода Т0 – через напряжение материала провода σ0 = ?0/F и фактическую суммарную площадь сечения проволок, составляющих провод, F, получим расчетную формулу для стрелы провеса провода, м:
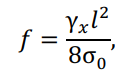
где γx – удельная вертикальная нагрузка провода, соответствующая условиям расчета провода, Н/м3;
σ0 – напряжение при растяжении в низшей точке провода. Соответствующее тем же условиям расчета, Па (10-7кгс/мм2);
l – длина пролета, м.
Выражение для стрелы провеса представляет собой уравнение параболы с хордой l и стрелой f. Тогда длина дуги такой параболы, а, следовательно, и длина провода в пролете будет:
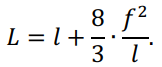
Длина провода в пролете отличается от длины пролета менее чем на 0,1%, т.е. на очень малую величину. Таким образом, сделанное ранее допущение о равномерном распределении нагрузки не по длине провода, а по длине пролета не приводит к заметной погрешности.
Напряжение в материале провода по его длине неодинаково в различных точках пролета. В низшей точке провеса провода оно меньше всего (σ0), а у точек закрепления провода на опоре оно под воздействием вертикальных нагрузок провода на участках ОА или ОВ достигает наибольшей величины (σ?). Для определения наибольшей величины напряжения в материале провода служит формула:
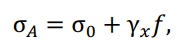
где γ? – удельная механическая нагрузка на провод.
В пролетах нормальной длины разница между σA и σ0 очень мала (не больше 0,3%) и ею обычно пренебрегают, используя для расчетов данные по напряжению в низшей точке провеса провода. Но при очень больших пролетах (порядка 500 м и более) необходимо применять приведенную выше формулу.
1. Условия максимального напряжения в проводе и максимальной стрелы провеса
Согласно ПУЭ для каждой марки провода, используемых при сооружении воздушной линии электропередачи, назначаются три значения допускаемого напряжения соответственно для трех возможных наиболее тяжелых режимов работы, отличающихся значениями величин внешних воздействий (давление ветра, гололедные отложения, температура окружающей среды) и, как правило, несовпадающими по временам года. Повторяемость перечисленных неблагоприятных факторов и вероятность их возникновения неодинакова. Кроме того, значения величин наибольших нагрузок, согласно картам ветрового напора и гололедных образований ПУЭ, являются различными для разных географических районов и местностей сооружения воздушных линий.
Максимальное напряжение в материале провода воздушной линии электропередач (ВЛ) может наступить при одном из следующих двух условий:
- при низшей температуре в данной местности, ϑмин;
- при наибольшей добавочной нагрузке и соответствующей этой нагрузке температуре окружающего воздуха при гололеде, ϑг, обычно равной минус 5℃, но иногда лежащей в пределах минус 5 до минус 10℃.
В первом случае увеличение тяжения по проводу происходит за счет сокращения его длины при низшей температуре, а во втором – за счет действия наибольших добавочных нагрузок (гололед, ветровой напор). При расчетах прежде всего выясняют, какой из этих случаев будет наиболее тяжелым для данного провода, а затем, исходя из допустимого напряжения в проводе в этом, более тяжелом случае, определяют напряжения для всех других условий работы провода в пролете.

Рис. 2. Гололедное образование на проводе ВЛ
Первый случай – для малых пролетов, когда в пределе значение длины пролета l = 0. Подставим значение l в уравнение состояния провода и, упростив его, получим:
![]()
где величины с индексом m относятся к известному (исходному) состоянию провода;
ϑ − искомая температура окружающей среды;
Е – модуль упругости, Н/мм2.
α −коэффициент неравномерности распределения скоростного ветрового напора по длине ВЛ.
При заданном скоростном напоре ветра, ?н, (Н/м2) коэффициент неравномерности распределения скоростного напора по длине ВЛ равен:
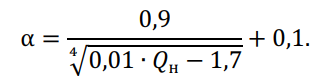
Из уравнения для первого случая видно, что при малых длинах пролетов расчетным является условие низшей температуры. Уравнение состояния провода для этого случая, после подстановки в него вместо σ? величины σдоп = σмакс будет иметь вид:
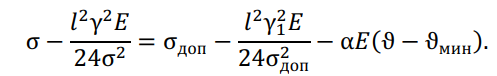
Второй случай – для больших пролетов, когда в пределе ? = ∞. Разделим уравнение состояния провода на ?2 и, упростив его, получим:
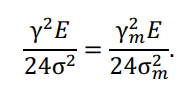
Из этого уравнения следует, что при больших длинах пролетов расчетным является условие наибольшей добавочной нагрузки, для которого уравнение состояния провода будет
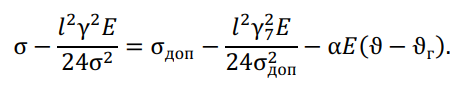
В соответствии с полученным уравнением, искомые напряжения в проводе зависят от длины пролета линии l. Можно подобрать пролет такой длины, при которой напряжения в проводе, как при низшей температуре, ϑмин, так и при наибольшей добавочной нагрузке γ7, будут одинаковыми, такой пролет называют критическим (lкр) при соответствующих условиях:
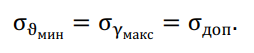
Совместное решение уравнений относительно ? = ?кр дает длину критического пролета:
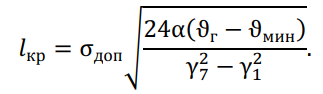
Сравнивая длину заданного (расчетного) пролета с длиной критического пролета, полученного из уравнения, можно установить, в каком из двух расчетных случаев материал провода испытывает большее напряжение.
Если заданный пролет меньше критического, то максимальное напряжение в проводе будет при низшей температуре окружающего воздуха ϑмин и удельной нагрузке γ1. Если заданный пролет больше критического, то максимальное напряжение в проводе будет при наибольшей удельной нагрузке γ7 и температуре ϑг.
Различают 3 критических пролета ?кр ?:
— ?кр1 –первый критический пролет – определяет переход от расчетных условий при наинизшей температуре к средним эксплуатационным условиям (СГ), при этом выполняются условия:
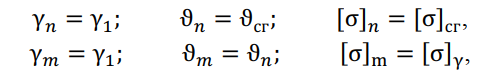
— ?кр2 –второй критический пролет – определяет переход от расчетных условий наинизшей температуры к условиям наибольшей нагрузки (НБ):
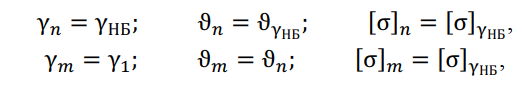
— ?кр3 – третий критический пролет – определяет переход от расчетных средних эксплуатационных условий(СЭ) к условиям наибольшей нагрузки:
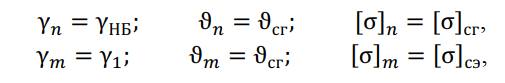
где величины с индексом m относятся к известному (исходному) состоянию провода, а с индексом n – к искомому состоянию.
Исходные условия расчета проводов на механическую прочность, соотношения расчетного и критического пролетов в зависимости от наинизшей температуры и наибольшей нагрузки приведены в табл. 1.
Одной из величин, определяющих высоту опор, является стрела провеса провода. Наибольшая стрела провеса провода, называемая максимальной стрелой провеса, может возникнуть только при отсутствии ветра, когда провод находится в вертикальной плоскости, проходящей через точки его крепления. Такой случай может быть:
а) — при гололеде и температуре от 0 до минус 10℃, когда провод испытывает наибольшую вертикальную нагрузку (γ3);
б) — при высшей температуре окружающего воздуха, например, при значении максимальной температуры ϑмакс = +40℃, когда провод имеет минимальное механическое напряжение и испытывает вертикальную нагрузку только от собственной массы (γ1).
Таблица 1. Условия расчета проводов на механическую прочность
| Соотношения
критических пролетов |
Соотношения расчетного
и критического пролетов |
Исходные условия
расчета проводов на механическую прочность |
| ?кр1 < ?кр2 < ?кр3 | ? < ?кр1 | ϑ(−) — Наинизшая температура |
| ?кр1 < ? < ?кр3 | СЭ — Средние эксплуатационные | |
| ? > ?кр3 | γНБ — Наибольшая нагрузка | |
| ?кр1 > ?кр2 > ?кр3 | ? < ?кр2 | ϑ(−)— Наинизшая температура |
| ? > ?кр2 | ? > ?кр3 — Наибольшая нагрузка |
Температура, при которой стрела провеса провода fп1, вызываемая только его собственной массой, будет равна стреле провеса провода в условиях гололеда без ветра fп3, называется критической температурой ϑкр. Значение последней определяется по формуле, полученной для случая ?п3 = ?п1. Путем сравнения значения ϑкр с высшей температурой ϑ(+) выявляются габаритные климатические условия. Приближенное значение критической температуры вычисляется по формуле:
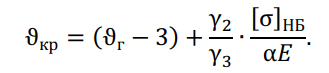
Чтобы определить, в каком случае будет максимальная стрела провеса, сравнивают величину высшей температуры данной местности с величиной критической температуры. Поскольку расчет механической прочности проводов все равно требует определения напряжения в проводе при высшей температуре и при гололеде без ветра, то, применяя эту формулу, можно значительно проще определить и сопоставить стрелы провеса в интересующих нас условиях.
Если критическая температура меньше высшей температуры данной местности, то максимальная стрела провеса провода будет при высшей температуре. Если же критическая температура больше высшей температуры данной местности, то максимальная стрела провеса будет при гололеде без ветра.
Длина фазного провода (троса) в пролете при одинаковой высоте его крепления на смежных опорах и пролетах до 800 м вычисляется как для параболы:
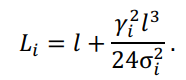
или при более длинных пролетах – как для цепной линии
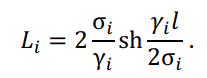 .
.
При неодинаковых высотах точек крепления проводов на опорах ВЛ их длина в пролете определяется по формуле:
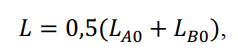
т.е. в виде суммы длин провода в половине пролета до разных точек крепления.
2. Расчёт удельных механических нагрузок от атмосферных воздействий на фазные провода и грозозащитные тросы с учетом высот их крепления на промежуточной опоре
Расчёт удельных механических нагрузок от атмосферных воздействий на фазные провода и на грозозащитные тросы рассмотрим на примере сталеалюминиевого провода, состоящего из двух слоев (рис. 3). Конструктивные данные сталеалюминевого провода, приведенные ниже, выбранной марки определяем по справочным данным.
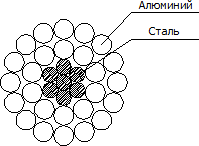
Рис. 3. Поперечное сечение сталеалюминиевого провода
В справочнике для сталеалюминиевого провода приводятся следующие параметры:
- ?? — нормативный диаметр провода марки АС, мм;
- ?? — диаметр стальной проволоки, мм;
- ?? — диаметр алюминиевой проволоки, мм;
- ?? — количество стальных проволок в проводе АС;
- ?? — количество алюминиевых проволок в проводе АС;
- M — масса 1 км провода, кг.
Сечения стальной и алюминиевой частей сталеалюминевого провода соответственно равны:
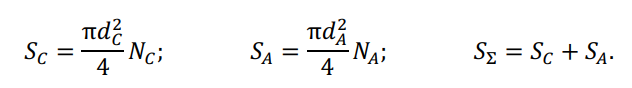
Соотношение сечений стальной и алюминиевой частей:
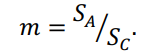
В зависимости от заданного климатического района определяют:
- максимальный нормативный скоростной напор ветра на высоте до 15 м над поверхностью земли (например, в IV-м ветровом районе его принимают равным 650 Н/м2);
- нормативную толщину стенки гололеда для высоты 10 м над поверхностью земли (во II-м гололедном районе составляет 10 мм);
- наименьшее допустимое расстояние от проводов до поверхности земли для ненаселенной местности, в зависимости от уровня напряжения.
На сооружаемых ВЛ, как правило, применяются унифицированные и типовые опоры для данных климатических условий территории страны, в зависимости от населенной или ненаселенной местности. Паспортные данные опоры должны соответствовать перечисленным в таблице 2.
Строительная высота гирлянды изоляторов ? выбирается в зависимости от уровня напряжения воздушной линии электропередачи и может изменяться в пределах (0,7 ÷ 4,9) м.
Таблица 2. Стальная промежуточная одноцепная опора ВЛ 110 кВ
| Ном.
напряж. |
Шифр | Условное
обозначение |
Марка
провода |
Толщина
стенкигололеда, мм |
Длина пролета, м | Расход
материалов |
||
| Габаритная | Весового | Ветрового | Стали,
кг |
|||||
| 110кВ | П110-3 | П-1Ц-Ст-С | с
АС-120/19 по АС-240/32 |
5, 10 | 365-440 | 155-555 | 435-445 | 2558 |
Расчет удельных механических нагрузок от атмосферных воздействий на фазные провода ВЛ проводится по следующему алгоритму:
— определяется постоянно действующая нагрузка от собственной массы провода:
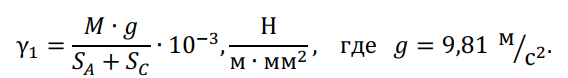
— рассчитывается временно действующая нагрузка от массы гололедных отложений:
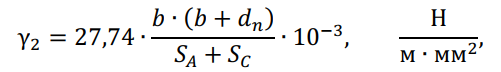
где: ? = ?н ∙ ??? ∙ ??ℎ — расчетная толщина стенки гололедного цилиндра на проводе, мм;
?н – нормативная толщина стенки гололеда;
![]() – поправочный коэффициент, учитывающий отличие диаметра провода от 10 мм;
– поправочный коэффициент, учитывающий отличие диаметра провода от 10 мм;
![]() – поправочный коэффициент, учитывающий отличие высоты расположения приведенного центра тяжести проводов, ℎцт∗ от 15 м;
– поправочный коэффициент, учитывающий отличие высоты расположения приведенного центра тяжести проводов, ℎцт∗ от 15 м;
Приведенный центр тяжести проводов, ℎцт∗ определяется с учетом расположением проводов на опоре:
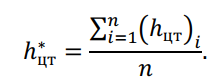
Для нижних проводов с учетом стрелы провеса:
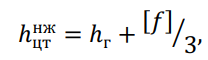 , где
, где
[?] = ?трнж — ℎг — λ – наибольшая стрела провисания провода;
?трнж – высота траверсы опоры.
Приведенный центр тяжести всех проводов ℎцт∗ определяется по формуле:
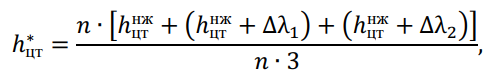
где ∆λ1 – расстояния между нижним проводом и вторым проводом;
∆λ2 – расстояния между нижним проводом и третьим проводом;
N – количество цепей в ЛЭП.
По вычисленным значениям удельных нагрузок γ1 и γ2 определяют суммарную вертикальную удельную нагрузку от собственной массы провода и массы гололеда:
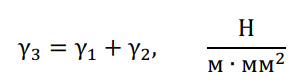
Затем определяют временно действующую горизонтальную нагрузку от давления ветра на провод, свободный от гололеда:
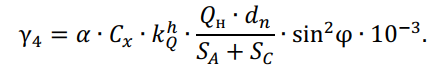
При заданном скоростном напоре ветра ?н, (Н/м2), коэффициент неравномерности распределения скоростного напора по длине ВЛ равен:
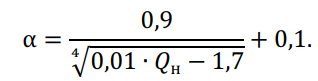
Значение аэродинамического коэффициента ?? зависит от ?? — нормативного диаметра провода марки АС (справочно). Поправочный коэффициент на высоту ??ℎ = 1 , при значении ℎцт∗ < 15 м при необходимости уточняется по справочнику.
В первом приближении при расчете коэффициента γ4 принимаем, что вектор скорости ветра направлен перпендикулярно проводам, тогда sin φ = 1.
Временно действующая горизонтальная нагрузка от давления ветра на провод, покрытый гололедом:
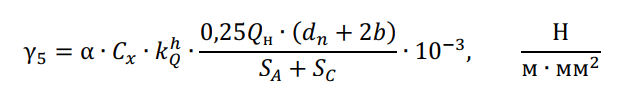
Результирующая удельная нагрузка от собственной массы провода и давления ветра:
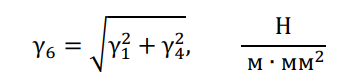
Завершающим этапом расчета является определение результирующей удельной нагрузки на фазные провода или трос от массы провода, массы гололеда и давления ветра:
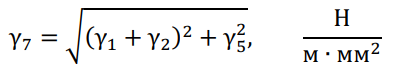
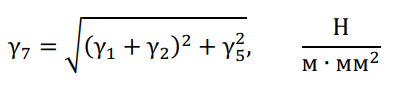
Сравнение удельных нагрузок с учетом сочетаний массы провода, массы гололеда и давления ветра позволяет выявить наибольшую для данного региона и скорректировать параметры проводов воздушной линии.
Расчёт удельных механических нагрузок на грозозащитные тросы производится аналогичным способом, как и расчёт фазных проводов, конструктивные данные которых, приводятся в справочниках. Однако при вычислении приведенного центра тяжести троса ℎцтт необходимо учитывать высоту подвеса троса, т.е. высоту опоры ?оп:
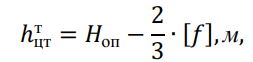
т.е. учесть отличие высоты расположения приведенного центра тяжести троса от 15 м.
2.1. Расчет однородных (монометаллических) проводов
Исходным условием расчета грозозащитных тросов в нормальных режимах является обеспечение допустимой стрелы провеса при климатических условиях, соответствующих атмосферным перенапряжениям, принимают, что при данных условий А для надежной защиты проводов от непосредственного поражения молнией стрела провеса троса должна быть на 0,5 – 1,5 м меньше стрелы провеса провода (0,5 м – пролет 200 – 250 м; 1,5 м – пролет 450 – 500 м).
![]()
Кроме того, расстояние между верхним проводом и грозозащитным тросом в середине пролета в нормальном режиме работы линии должно быть не менее следующих значений (высота между проводом и тросом):
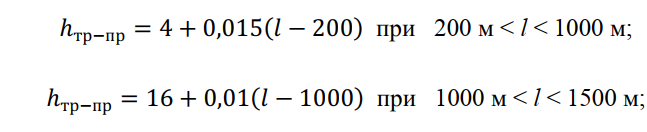
По стреле провеса троса определяется его механическое напряжение при климатических условиях соответствующих атмосферным перенапряжениям:
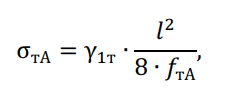
где, γ1т – удельная нагрузка троса от его собственной массы, ![]() ;
;
l – длина пролета, м;
?тА – стрела провеса троса для условий А, м.
По найденному значению механического напряжения троса σтА и по уравнению состояния записанного для троса, определяется напряжение троса при любых климатических условиях:
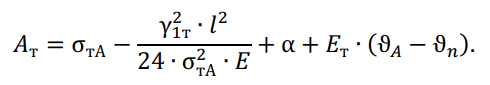
Температура воздуха при атмосферных перенапряжениях принимается равной 15℃.
Климатические условия для проверки на прочность стального грозозащитного троса устанавливается путем расчета 3-его критического пролета:
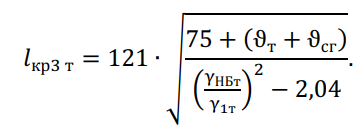
Если ? < ?кр3, то уравнение состояния троса рассчитывается при средних эксплуатационных условиях и сравнивается с соответствующим дополнительным уравнением. Если ? > ?кр3, то расчет троса ведется по наибольшей механической нагрузке.
Цель механического расчета провода – выявить условия, обеспечивающие создание в них необходимого запаса прочности. Поэтому допустимое напряжение в проводе принимается значительно меньше его предельного сопротивления при разрыве, т.е.
![]()
где п – коэффициент запаса прочности провода.
В ГОСТ 839-74 «Провода неизолированные для линий электропередачи» для всех марок и конструкций проводов даны разрывные усилия провода в кгс. На основании этих данных предельное сопротивление при разрыве для любого провода определится из формулы:
![]()
где R – разрывное усилие провода. кгс; F – фактическая суммарная площадь сечения проволок, составляющих провод, мм2.
Кроме расчета проводов по максимально допустимому напряжению σдоп рассчитывают напряжение в них при среднегодовой эксплуатационной температуре ϑэ и отсутствии внешних нагрузок. Это напряжение, обозначаемое через σэ, значительно меньше σдоп. Ограничение напряжения в проводе до значения σэ при среднегодовой температуре служит для предотвращения преждевременного износа провода от усталости из-за вибраций в нем.
Для определения величины σэ в уравнение состояния провода в пролете в качестве исходных условий (т.е. величин с индексом m) принимают условия, отвечающие максимальному напряжению провода (σмин или ϑг), и затем определяют σэ при подстановке в уравнение соответствующих этому условию значений γ1 и ϑэ (вместо γ и ϑ).
Таким образом, провода (монометаллические и комбинированные) рассчитывают для следующих условий:
- наибольшей внешней нагрузки;
- низшей температуры при отсутствии внешних нагрузок;
- среднегодовой температуры при отсутствии внешних нагрузок.
2.2. Тяжение по проводам и грозозащитным тросам при их разрывах
При обрыве провода (проводов) линии в одном из промежуточных пролетов снижается тяжение и напряжение в проводе той же фазы в неповрежденных промежуточных пролетах. При этом делается расчет приближения проводов к поверхности земли и усилий, воспринимаемых промежуточными опорами.
Наибольшее тяжение создается в проводе в промежуточном пролете примыкающем к анкерной опоре. Этот режим является расчетным для промежуточной опоры ограничивающей аварийный пролет.
При прохождении трассы ВЛ по населенной местности является обязательным обеспечение нормируемого приближения к землепровисных необорванных проводов. Для этих целей сокращается длина промежуточных пролетов, либо промежуточные опоры заменяются анкерными облегченными. Опоры до 1 кВ не рассчитываются по нагрузкам в аварийном режиме, для опор выше 1 кВ нормативное тяжение по проводам воспринимаемое промежуточной опорой определяется следующим образом:
- по таблице ПУЭ при креплении проводов в глухих зажимах;
- по паспортным данным зажимов при креплении проводов в зажимах с ограниченной прочностью заделки;
- принимается равным 1,5 кН для крепления проводов к штыревым изоляторам;
- рассчитывается на основе специальных методик.
При обрыве молниезащитного троса в одном из промежуточных пролетов тяжение по проводу в соседнем пролете определяется по следующей формуле:
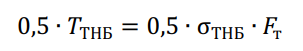
?ТНБ – наибольшее тяжение троса;
σТНБ – наибольшее напряжение троса;
?т – поперечное сечение троса.

