Механические свойства материалов при различных нагрузках

Механические свойства материалов являются фундаментальным аспектом инженерии и материаловедения, определяющим их способность сопротивляться внешним воздействиям, сохранять форму и функциональность в процессе эксплуатации. Изучение этих свойств позволяет прогнозировать поведение конструкционных элементов под воздействием разнообразных нагрузок, от медленно действующих (статических) до быстрых и циклических (динамических).

Понимание природы возникающих внутри материала напряжений и деформаций — ключ к проектированию надежных и долговечных конструкций, обеспечению безопасности и экономичности производства. Сегодня разнообразные методы испытаний, включая растяжение, измерение твердости, усталостные и другие тесты, позволяют получить комплексную картину механических характеристик материалов.

Изучение механических свойств материалов началось с древних времен, когда мастера стремились понять, почему одни материалы выдерживают нагрузки лучше других. Однако систематические исследования стали возможны лишь с развитием механики и материаловедения в XIX веке.

В 1820-х годах Роберт Гук сформулировал знаменитый закон упругости, описывающий линейную зависимость между нагрузкой и деформацией при небольших напряжениях. В XX веке развитие машиностроения и авиации вызвало потребность в точных методах испытаний, что привело к стандартизации тестов прочности и твердости.

В середине XX века были разработаны методы испытаний на усталость, что позволило значительно повысить безопасность и надежность ответственных конструкций. Современные технологии автоматизации и цифрового анализа обеспечивают высокую точность и оперативность при определении механических характеристик.

Нагрузки, изменяющиеся во времени, подразделяются на две ключевые группы: статические и динамические. К первой категории относят такие виды нагружения, при которых изменение силы происходит достаточно медленно. В отличие от них, динамические нагрузки отличаются значительной скоростью воздействия, как это бывает, например, при ударе или вибрациях.

В результате действия внешних нагрузок, а также изменений, происходящих в микроструктуре материала, внутри конструкционных элементов формируются внутренние напряжения. Эти напряжения являются реакцией материала на приложенные силы и зависят от как внешних условий, так и внутренних особенностей структуры.

Силы, воздействующие на элементы машин и различных сооружений, как правило, распределяются по объему или площади их поперечного сечения, что необходимо учитывать при расчетах прочности и устойчивости.

Для упрощённого понимания механики напряжений рассмотрим случай осевого растяжения цилиндрического стержня, изображённый на рис. 1, а. В этом варианте нагружения напряжение σ определяется простым соотношением: σ = Р/F₀, где Р — приложенная растягивающая сила, а F₀ — площадь поперечного сечения детали.

Если сила Р приложена не под прямым углом к сечению F₁, то полное напряжение σ₁ делится на две проекции: нормальное напряжение σ_n, действующее перпендикулярно плоскости, и касательное напряжение τ, параллельное этой поверхности.

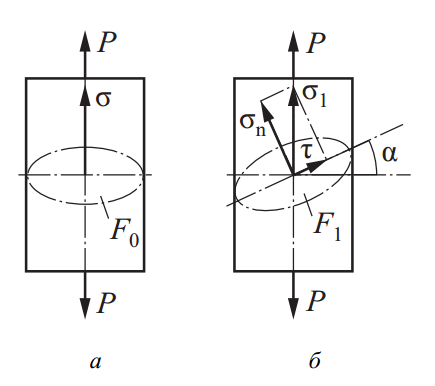
Рис. 1. Схема нормальных (а) и касательных (б) напряжений

На схеме рис. 1, б изображена наклонная плоскость сечения F₁, образующая угол α с осью цилиндра. Площадь этого наклонного сечения определяется как F₁ = F₀/cosα. Общее напряжение в данной плоскости выражается формулой σ₁ = Р/F₁ = σ cosα. Далее, в соответствии с векторной алгеброй, происходит разложение напряжения σ₁ на составляющие: нормальную σ_n = σ cos²α и касательную τ = σ cosα sinα, или же τ = 0,5σ sin2α. Максимальное значение σ_n достигается при α = 0°, тогда как максимальная величина τ наблюдается при угле 45°, и составляет она σ/2.

Применённая нагрузка вызывает деформацию тела, проявляющуюся в изменении его формы и размеров. В зависимости от характера поведения материала после снятия нагрузки различают несколько типов деформаций.

Если после снятия нагрузки тело полностью восстанавливает исходную форму, такая деформация классифицируется как упругая. В случае, когда изменения формы и объема сохраняются, речь идёт о пластической деформации, или остаточной.

При значительных нагрузках, превышающих предел упругости, развивается упругопластическая деформация, которая в предельных ситуациях может завершиться разрушением материала конструкции.

Разрушение — это необратимый процесс, включающий образование и развитие трещин, приводящий в конечном итоге к разделению материала на части. Существуют два основных сценария разрушения: хрупкий и вязкий.

При хрупком разрушении доминирующую роль играют нормальные напряжения, которые вызывают быструю и неконтролируемую (нестабильную) трещину. Такая трещина развивается самостоятельно и практически мгновенно охватывает материал.

В противоположность этому, при вязком разрушении преобладают касательные напряжения, способствующие возникновению значительной пластической зоны у вершины трещины. В этой зоне материал деформируется, и сама трещина теряет остроту, что снижает скорость её распространения.

Одной из определяющих характеристик вязкого разрушения является малая скорость роста трещины. Для сравнения: хрупкая трещина в конструкционной стали способна развиваться со скоростью до 2500 м/с, что часто провоцирует внезапное и катастрофическое разрушение конструкции.

Для изучения механических свойств металлических материалов, особенно при действиях переменных и кратковременных нагрузок, используются разнообразные методы испытаний. Наиболее востребованными считаются статические тесты на растяжение и измерения твёрдости.

Кроме того, применяются дополнительные испытания, направленные на определение усталостной прочности, ползучести и износостойкости. Эти методы позволяют более всесторонне оценить эксплуатационные характеристики материалов и предсказать их поведение в различных условиях.

1. Механические свойства при статических нагрузках

Испытания на растяжение. Этот метод занимает центральное место в системе испытаний металлов, так как позволяет выявить ключевые характеристики: прочность, упругость и пластичность материала при воздействии медленно возрастающих нагрузок.

Прочностью называется способность твердого материала выдерживать как статические, так и динамические воздействия без разрушения или чрезмерной деформации. Для проведения испытаний готовят стандартизованные образцы, выполненные из изучаемого материала, форма и размеры которых строго регламентированы.

В ходе испытаний на растяжение по ГОСТ 1497–84, образец подвергается продольной нагрузке, при которой он остается в равновесии, а возникающие в теле напряжения увеличиваются до момента разрушения. Обычно используют круглые образцы (рис. 2, а), либо плоские — для материалов листового проката. Конструкция образца включает рабочую часть и захватываемые головки. Важным параметром образца является его кратность — отношение начальной расчетной длины l₀ к начальному диаметру d₀, для которой применяются значения 2,5; 5 и 10.

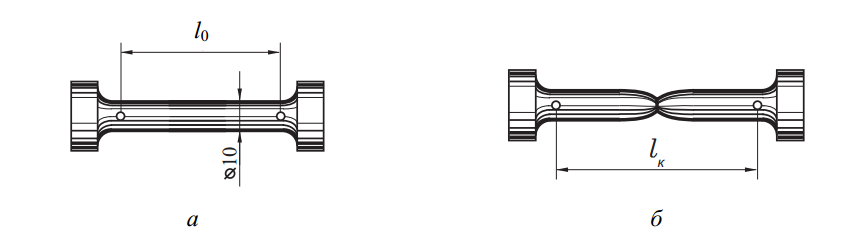
Рис. 2. Образцы испытуемого металла на прочность и пластичность при растяжении: а – до испытания; б – после испытания

Сегодняшние модели разрывных машин автоматизированы: они формируют диаграммы деформации, которые отображаются и сохраняются в цифровом виде на компьютере. По мере увеличения нагрузки наблюдаются визуальные и числовые характеристики растяжения вплоть до момента разрушения образца.

Растягивающее усилие вызывает удлинение материала, а при достижении предельного напряжения происходит разрыв. На рисунке 3 представлена диаграмма растяжения низкоуглеродистой стали. По вертикальной оси отложено усилие P в меганьютонах, а по горизонтальной – абсолютное удлинение ∆l в миллиметрах. Данная кривая отражает поведение металла под действием медленно возрастающей нагрузки.

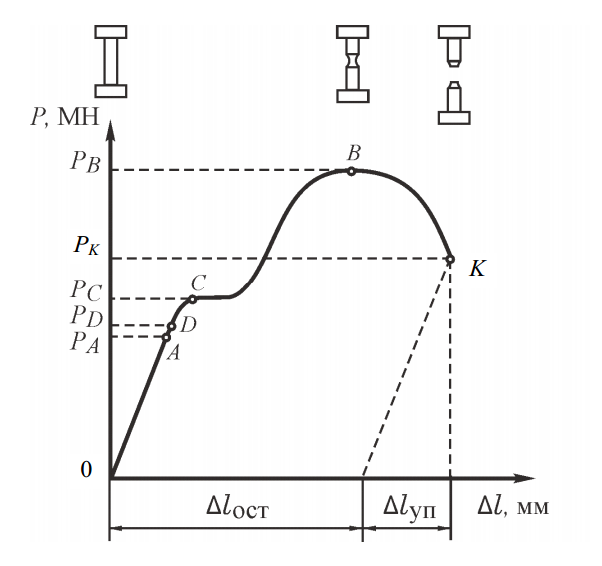
Рис. 3. Диаграмма растяжения пластичного металла

Напряжение σ (МПа) вычисляется как результат деления силы Р на исходную площадь поперечного сечения F₀:

σ = Р / F₀.

Начальный участок диаграммы (0А) отображает прямолинейную зависимость между нагрузкой и удлинением. Эта зона соответствует пределу пропорциональности Р_пц, при котором деформация линейно подчиняется увеличению усилия. Точка А ограничивает зону, где соблюдается закон Гука.

После точки А диаграмма приобретает кривизну, указывая на начало упругих, но уже нелинейных деформаций. До точки D материал сохраняет способность к полному восстановлению формы после снятия нагрузки. Величина напряжения в этой точке соответствует пределу упругости и вычисляется следующим образом:

σ_упр = PD / F₀.

Точка С сигнализирует о начале площадки текучести — фрагмента диаграммы, где удлинение продолжается при практически постоянной нагрузке. Напряжение в этой точке называется пределом текучести σ_т:

σ_т = P_С / F₀,

где P_С – усилие в точке начала площадки текучести.

Важно отметить, что текучесть присуща преимущественно пластичным металлам, например, низкоуглеродистой отожженной стали или отдельным маркам латуни. У сталей с высоким содержанием углерода и прочих металлов, у которых отсутствует площадка текучести, применяют расчет условного предела текучести σ_0,2. Это напряжение, при котором происходит остаточная деформация, равная 0,2 % расчетной длины:

σ_0,2 = Р_0,2 / F₀.

Далее по диаграмме следует точка В, указывающая на максимальное значение нагрузки до разрушения. Соответствующее напряжение называется временным сопротивлением разрушению или пределом прочности σ_В:

σ_В = Р_max / F₀,

где Р_max – наибольшая зафиксированная нагрузка.

В момент разрушения, соответствующий точке K, сохраняется только остаточная деформация. Упругая часть удлинения ∆l_уп исчезает. Она определяется отрезком между началом координат и нормалью, опущенной из соответствующей точки кривой на ось абсцисс. Фиксируемое значение абсолютного остаточного удлинения ∆l_ост отражает степень пластичности испытуемого материала.

Пластичность представляет собой способность материала изменять свою форму и размеры после снятия нагрузки без разрушения. Эта характеристика количественно оценивается по двум показателям — относительному удлинению δ и относительному сужению поперечного сечения Ψ.

Значение δ в процентах вычисляется по следующей формуле:

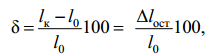
где l_к – длина после разрыва; l₀ – исходная длина образца.

Второй показатель — Ψ — рассчитывается следующим образом:

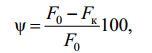
где F₀ – исходная площадь поперечного сечения, F_к – площадь в месте разрыва.

У хрупких металлов значения δ и Ψ малы, зачастую стремятся к нулю. В то же время, у пластичных материалов эти показатели могут достигать десятков процентов, демонстрируя хорошую деформируемость.

Еще одной важной характеристикой является модуль упругости E, который показывает отношение возникающего напряжения к соответствующему удлинению в пределах упругих деформаций (участок 0В):

E = σ / δ.

Данный модуль отражает жесткость металла и его способность сопротивляться упругой деформации.

Итак, благодаря методике растяжения при статических нагрузках удается определить важнейшие механические свойства металлов — их прочность, упругость и пластичность, которые лежат в основе проектирования и расчета конструкционных элементов.

В отличие от прочностных параметров, оценка твердости проводится значительно быстрее, не требуя изготовления специальных стандартных образцов. Это делает методику особенно удобной для массового применения в производственных условиях.

Твердость – характеристика, определяющая способность материала сопротивляться внедрению в его поверхность другого тела, которое само при этом не подвергается остаточным деформациям. Эта величина тесно связана с прочностью и позволяет в ряде случаев делать косвенные выводы о других механических свойствах сплава или металла.

В промышленной практике наибольшее распространение получили методы, основанные на вдавливании индентора (твердого наконечника) в поверхность образца. Эти методы позволяют получить количественные значения твердости с высокой степенью достоверности.

Метод Бринелля регламентирован ГОСТ 9012-59 и относится к числу стандартных. В данном способе испытания используют закалённый стальной шарик диаметром D (1, 2, 2,5, 5 или 10 мм), который под действием силы Р вдавливают в поверхность исследуемого материала (рис. 4, а). После удаления шарика остается отпечаток в виде лунки диаметром d, величина которого обратно пропорциональна твердости исследуемого материала (рис. 4, б).

Величина твердости по Бринеллю (обозначается НВ) рассчитывается по выражению:

НВ = P / F,

где P – прикладываемая сила, Н; F – площадь отпечатка на поверхности, мм². Численное значение НВ указывается без единиц измерения, например: 185 НВ.

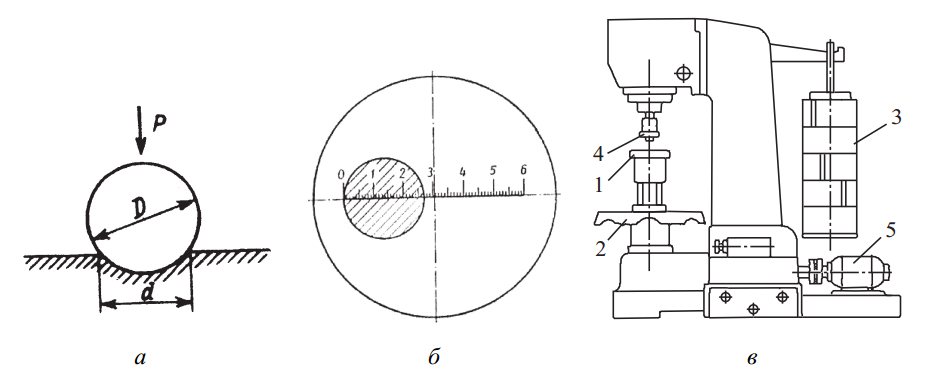
Рис. 4. Определение твердости: а – принцип испытания по Бринеллю; б – след шарика на поверхности; в – оборудование для выполнения испытаний

Проведение испытаний осуществляется с учетом рекомендованных нагрузок, соответствующих применяемому диаметру шарика. Для проведения измерений по Бринеллю широко используются прессовые установки типа ТШ (рис. 4, в). По данному методу возможно определение твердости материалов до 450 НВ включительно. Стандартные значения (например, 185 НВ) соответствуют нагрузке 30 000 Н и диаметру индентора 10 мм.

Метод Роквелла, описанный в ГОСТ 9013-59, отличается более высокой скоростью выполнения и универсальностью. В качестве индентора может использоваться либо алмазный конус с углом 120°, либо шарик диаметром D = 1,58 мм (1/16 дюйма).

Образец размещают на столике 3 прибора ТК (рис. 5), после чего при помощи маховика 4 он подводится к наконечнику (2). При достижении предварительной нагрузки 100 Н активируется основная нагрузка с помощью рычага 5. Через 5–6 секунд вдавливания основная нагрузка снимается, и производится считывание результата.

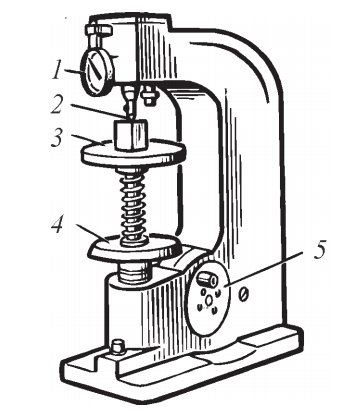
Рис. 5. Прибор для измерения твердости по Роквеллу: 1 – шкала индикатора; 2 – наконечник (алмазный или шариковый); 3 – стол; 4 – маховик; 5 – управляющая рукоятка

Твердость по Роквеллу определяется разницей между глубиной проникновения наконечника при предварительной и полной нагрузках. При этом одно деление шкалы соответствует проникновению индентора на глубину 2 мкм. Обозначение твердости включает числовое значение и индекс шкалы: HRА, HRB или HRC.

Шкала A: используется алмазный наконечник и нагрузка 588 Н. Применяется при измерении твердости тонких покрытий, листовых материалов и особенно твердых образцов. Диапазон измерений: 70–85 HRA.

Шкала B: задействован стальной шарик и нагрузка 981 Н. Метод ориентирован на мягкие материалы, твердость которых не превышает 400 НВ. Диапазон: 25–100 HRB.

Шкала C: алмазный конус и нагрузка 1 472 Н. Используется для твердых сталей и закаленных поверхностей, твердость которых превышает 450 НВ. Диапазон: 20–67 HRC.

Следует отметить, что значения твердости, полученные методами Бринелля и Роквелла, напрямую не сопоставимы и не могут быть переведены из одной системы в другую с высокой точностью.

Метод Виккерса, согласно ГОСТ 2999–75, основывается на вдавливании четырехгранной алмазной пирамиды с углом 136º в испытуемый материал. После снятия нагрузки отпечаток имеет форму квадрата (рис. 6), диагональ которого измеряется и используется для определения значения твердости.

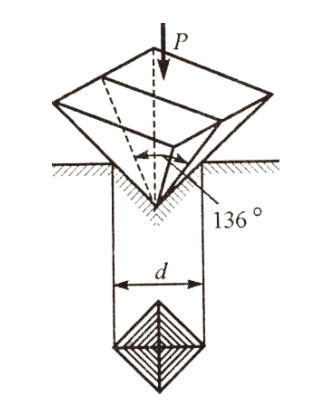
Рис. 6. Схема определения твердости по Виккерсу

Значение твердости вычисляют по таблицам, используя измеренные размеры отпечатка и соответствующую нагрузку. На практике метод применяют для анализа твердых сплавов, тонких защитных покрытий, а также компонентов малых сечений. Стандартные нагрузки варьируются от 10 до 500 Н. При уменьшении толщины исследуемого слоя снижается и нагрузка.

Для материалов с твердостью до 450 НВ результаты испытаний по Бринеллю и по Виккерсу практически совпадают, что позволяет использовать эти методы взаимозаменяемо в ряде случаев.

2. Механические свойства при динамических нагрузках

В условиях эксплуатации деталей машин нередко возникают динамические нагрузки, под воздействием которых многие металлические материалы склонны к хрупкому разрушению. Особенно опасными в таких ситуациях оказываются надрезы, выступающие в роли концентраторов напряжений.

Чтобы выявить степень восприимчивости материала к разрушению в подобных условиях, проводят специальные испытания — ударные испытания на маятниковых копрах (рис. 7, а). Стандартный образец, соответствующий требованиям ГОСТ 9454–78, фиксируют на двух опорных точках и наносят удар в центральной части, вызывающий разрушение (рис. 7, б).

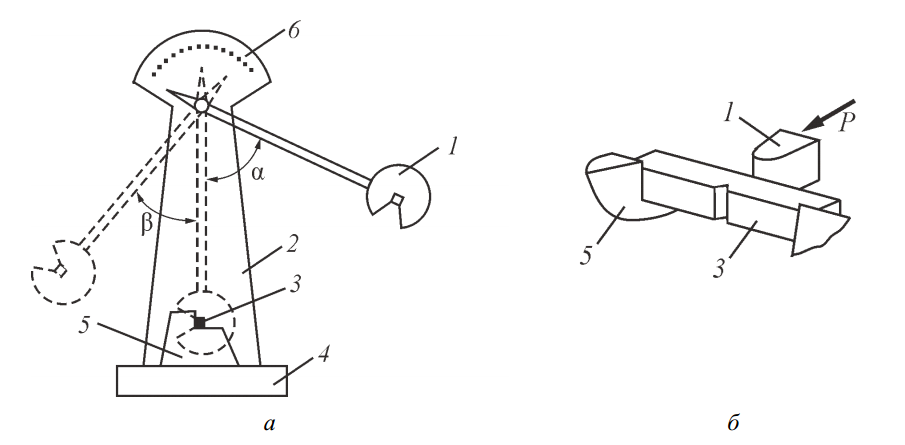
Рис. 7. Схема проведения ударных испытаний: а – маятниковый копер: 1 – нож; 2 – стойка; 3 – образец; 4 – основание; 5 – опоры образца; 6 – шкала; б – ударный изгиб образца с V-образным надрезом

Показания шкалы копра позволяют определить количество энергии K, Н, затраченной при разрушении, на основании чего вычисляется ключевой параметр — ударная вязкость. Эта величина рассчитывается по формуле:

KC = K / S₀¹,

где S₀¹ — площадь сечения образца в месте выполнения надреза.

Результат измеряется в мегаджоулях на квадратный метр (МДж/м²), что отражает энергию, приходящуюся на единицу разрушенного сечения.

В зависимости от формы надреза различают три типа образцов: с U-образным надрезом (радиус r = 1 мм), с V-образным (радиус r = 0,25 мм) и с Т-образной формой надреза, дополнительно упрочнённой искусственно сформированной усталостной трещиной. Соответствующие показатели ударной вязкости маркируются как KСU, KСV и KСТ.

Основной характеристикой, широко применяемой при технических расчётах, выступает KСU. Этот показатель включает в себя два компонента:

KСU = KС₃ + KС_р,

где KС₃ отражает энергию, необходимую для инициирования трещины, а KС_р (приблизительно равный KСТ) соответствует работе, затраченной на её распространение по телу образца.

Следует отметить, что уменьшение радиуса надреза приводит к снижению значения KС₃, поскольку инициация трещины при более резком концентраторе требует меньших затрат энергии. Показатель KСТ при этом служит критерием трещиностойкости, то есть отражает устойчивость материала к росту уже возникшей трещины.

Наибольшую чувствительность к изменению температуры среди всех механических характеристик проявляет именно ударная вязкость. Именно по этой причине испытания при пониженных температурах широко используются для определения переходного температурного диапазона, называемого порогом хладноломкости. В этом диапазоне наблюдается резкое снижение способности материала сопротивляться ударным нагрузкам.

Хладноломкость — это склонность металлов терять вязко-пластические свойства и разрушаться хрупко при охлаждении. Признаками перехода к хрупкому разрушению являются не только резкое падение значений ударной вязкости, но и изменение характера излома образца. Уровень порога хладноломкости может быть представлен либо конкретной температурой t₅₀, при которой значение KСТ падает до 50% от исходного, либо определённым температурным интервалом.

3. Механические свойства при переменных (циклических) нагрузках

В процессе эксплуатации множество элементов машин — такие как шатуны, валы, зубчатые пары — подвергаются многократному действию переменных (циклических) нагрузок, которые могут существенно отличаться по форме, частоте и амплитуде.

Цикл напряжения представляет собой последовательное изменение уровня напряжения от минимального значения σ_min до максимального σ_max и обратно за определённый промежуток времени Т. В лабораторной практике изучения усталостной прочности материалов за основу чаще всего берут синусоидальный характер изменения напряжения, как представлено на рис. 8, а. Основной характеристикой здесь является коэффициент асимметрии R = σ_min / σ_max.

Циклы делятся на симметричные (R = -1) и несимметричные (при других значениях R), что определяет разные условия и режимы работы конструктивных элементов.

Явление постепенного ухудшения прочностных свойств материала при длительном действии циклической нагрузки, сопровождающееся зарождением, развитием трещин и последующим разрушением, называется усталостью, а способность материала сопротивляться этому процессу — выносливостью.

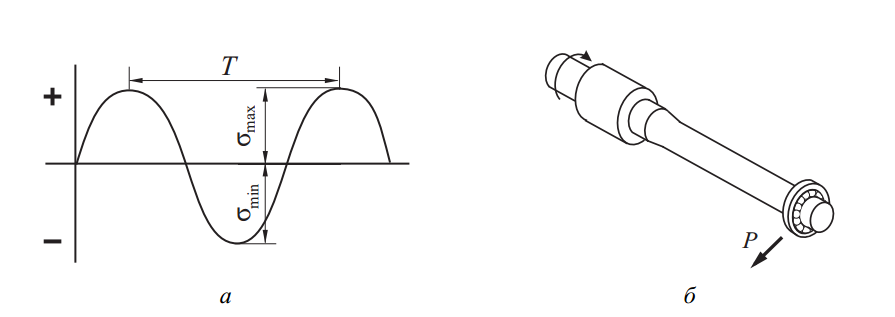
Рис. 8. Схема испытаний на усталость: а – график циклического напряжения; б – испытуемый образец

Особенности разрушения при усталости отличаются от разрушения при статических нагрузках:

1. Оно может происходить при значительно меньших напряжениях, чем предел текучести или разрушающее напряжение при одноразовой нагрузке.
2. Зарождение разрушения начинается на поверхности или вблизи неё в местах, где концентрируются напряжения. Эти зоны концентраторов могут образовываться как в результате эксплуатации, так и из-за дефектов обработки (царапины, надрезы и др.).
3. Само разрушение проходит по стадиям: от накопления микроповреждений до образования и роста одной основной усталостной трещины, завершающейся полным разрушением.
4. Излом имеет чёткую зональность: очаг разрушения, усталостную зону и область окончательного долома (рис. 9, а), каждая из которых свидетельствует о фазах разрушения.

Очаг разрушения — это начальная область, расположенная у поверхности, имеет гладкую структуру и малую площадь. За ним следует зона усталости, по структуре напоминающая слоистые кольца или борозды, которые фиксируют ступенчатое продвижение трещины.

Завершающая часть разрушения — зона долома — формируется в момент, когда оставшееся сечение материала становится неспособным воспринимать действующее напряжение, что приводит к мгновенному разрушению оставшейся части конструкции (рис. 9, а).

Для определения способности материалов выдерживать циклические нагрузки проводят испытания на специальных установках, обеспечивающих циклы растяжения-сжатия, кручения или изгиба. Испытания выполняются с сериями образцов (обычно не менее 15), подвергающихся нагрузке на разных уровнях напряжения до разрушения.

Результаты таких испытаний представляют в виде так называемой кривой усталости. В логарифмической системе координат, где по оси X откладывается количество циклов N, а по оси Y – максимальное напряжение σ_max, строится зависимость, имеющая обычно два участка: наклонный и горизонтальный (рис. 9, б).

Горизонтальный отрезок отображает предел выносливости — напряжение, не вызывающее разрушения даже при очень большом числе циклов (или базовом значении N_σ). Для симметричных циклов это значение обозначается как σ_–1, а в общем случае — как σ_R, где R – коэффициент асимметрии цикла.

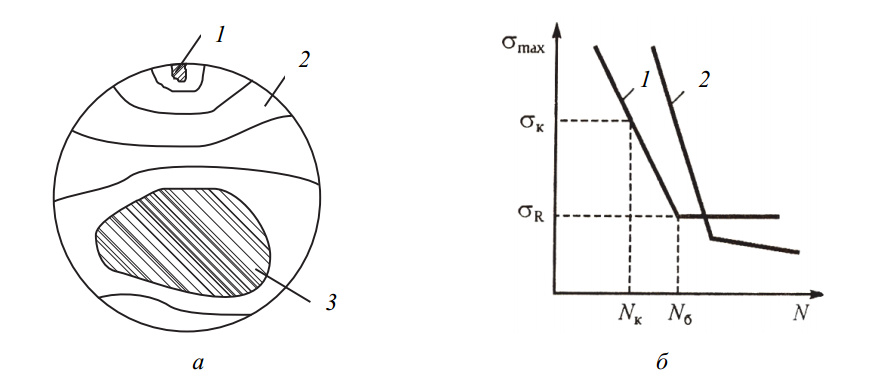
Рис. 9. Усталостное разрушение: а – схема развития излома: 1 – начало трещины; 2 – область усталости; 3 – зона долома; б – усталостные кривые: 1 – для стали; 2 – для цветных металлов

Наклонная часть кривой отражает ограниченную выносливость — напряжение, при котором разрушение всё же произойдёт, но спустя строго определённое число циклов.

Для сталей при умеренных температурах характерны кривые с чётким горизонтальным участком. В случае цветных металлов, а также конструкций, работающих в агрессивных или высокотемпературных условиях, горизонтального участка нет — такие материалы обладают лишь ограниченной усталостной прочностью (рис. 9, б).

На основании анализа кривых усталости можно сформулировать два основных показателя сопротивления усталости:

1. Циклическая прочность — максимально возможное напряжение, которое материал способен выдержать в течение определённого времени работы. Этот показатель отражает физический или условный предел выносливости.
2. Циклическая долговечность — это предельное число циклов (или соответствующее время эксплуатации), по истечении которого возникает трещина критической длины или происходит полное разрушение при заданном уровне напряжения.

Заключение

Интересные факты:

• Скорость распространения хрупкой трещины в некоторых сталях может достигать 2500 м/с — это почти в 7 раз быстрее скорости звука в воздухе!

• Метод Бринелля, изобретенный в 1900 году, до сих пор остаётся одним из самых распространенных и надежных способов определения твердости.

• Не все материалы ведут себя одинаково: например, стекло обычно разрушается хрупко, а сталь – вязко, что позволяет ей поглощать энергию и предотвращать катастрофические разрушения.

• Модуль упругости стали примерно в 200 раз превышает модуль упругости резины, что иллюстрирует колоссальную разницу в их способности сопротивляться деформации.

• Современные компьютерные методы моделирования все чаще дополняют физические испытания, позволяя прогнозировать механические свойства материалов еще на стадии проектирования.

Механические свойства материалов — краеугольный камень современной инженерии, влияющий на выбор материалов и проектных решений в самых разных отраслях. Статические, динамические и циклические нагрузки оказывают комплексное влияние на прочность, пластичность и устойчивость конструкционных элементов.

Методы испытаний, начиная с классических тестов на растяжение и измерения твердости, и заканчивая усталостными и износостойкими тестами, позволяют всесторонне оценить эксплуатационные характеристики материалов. Глубокое понимание механических свойств способствует разработке надежных, экономичных и долговечных изделий, что напрямую влияет на безопасность и эффективность технологий.

В будущем развитие новых материалов и совершенствование методик испытаний продолжат играть важнейшую роль в научно-техническом прогрессе.

• Об авторе
• Недавние публикации

Александр Лавриненко

Александр Лавриненко недавно публиковал (посмотреть все)

• Механические свойства материалов при различных нагрузках - 22.05.2025
• Износ механизмов в процессе трения: причины, последствия и методы оценки - 21.05.2025
• Современные смазочные материалы: их классификация, характеристики и применение - 03.05.2025