Содержание страницы
1. Математические модели линии
В установившемся режиме для нахождения взаимосвязи между параметрами режима в начале и конце линии обычно используют уравнения длинной линии
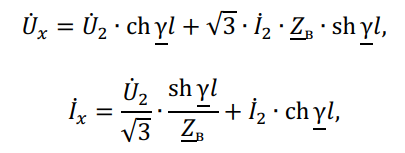
где ![]() и
и ![]() — соответственно линейное напряжение и фазный ток в точке х линии, удаленной на расстояние l от её конца;
— соответственно линейное напряжение и фазный ток в точке х линии, удаленной на расстояние l от её конца;
![]() и
и![]() – аналогичные напряжение и ток в конце линии длиной L;
– аналогичные напряжение и ток в конце линии длиной L;
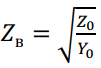 – волновое сопротивление линии;
– волновое сопротивление линии;
![]() − комплексные сопротивление проводимость единицы длины линии соответственно.
− комплексные сопротивление проводимость единицы длины линии соответственно.
Уравнения длинной линии можно использовать при следующих допущениях:
- трехфазная линия электропередачи представляет собой линейную симметричную электрическую цепь;
- тройки фазных векторов токов и напряжений образуют симметричные системы и являются строго синусоидальными функциями времени.
Допущение о линейности цепи предполагает, что ее параметры принимаются постоянными, не зависящими от параметров режима. В реальной линии, например, активное сопротивление зависит от протекающего по линии тока, а активная проводимость – от напряжения.
Допущение о симметричности цепи предполагает, что параметры различных фаз одинаковы, но большинство реальных линий сооружается с таким взаимным расположением проводов, которому соответствует различие параметров фаз. (для выравнивания параметров фаз – транспозиция проводов).
Допущения о синусоидальности кривых мгновенных значений токов и напряжений фаз, по существу, предполагает отсутствие в электрической системе элементов, являющихся источниками высших гармоник, а также идеальную синусоидальность ЭДС синхронных генераторов, что в действительности не имеет места или в должной мере не обеспечивается.
Введение перечисленных допущений отвечает вполне определенной идеализации реальной линии электропередачи. Однако мероприятия, осуществляемые в электрических системах по ограничению степени несимметрии и несинусоидальности в соответствии с требованиями межгосударственного стандарта ГОСТ 13109 – 97 по обеспечению качества электроэнергии, приводят к тому, что обусловленная принятыми допущениями степень идеализации линии, как элемента реальной электрической системы оказывается приемлемой не только для качественного, но и для количественного анализа, позволяя адектватно отразить ее свойства как в нормальных, так и в послеаварийных установившихся режимах, не связанных с пофазным отключением элементов системы.
В большинстве случаев устанавливается соотношение параметров режима линии по концам электропередачи. При этом полагая l = L , получим выражения для расчета параметров режима начала линии:
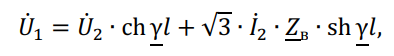
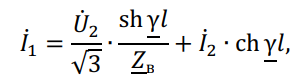
При качественном анализе пренебрегают активным сопротивлением и проводимостью и рассматривают «линию без потерь». При этом волновое сопротивление является вещественным числом, а коэффициенты – затухания равен нулю и распространения электромагнитной волны – чисто мнимое число.
При этом «уравнения длинной линии» упрощаются благодаря исключению гиперболических функций с учетом соотношений:
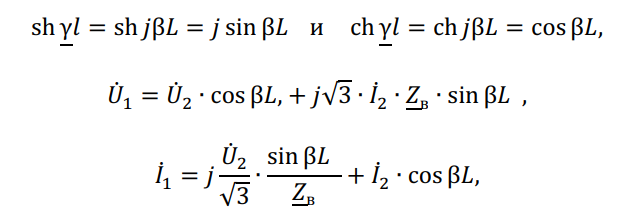
В общем случае линии электропередачи рассматриваются как линии с равномерно распределенными по её длине параметрами. В инженерных расчетах для воздушных линий электропередачи (ЛЭП) длиной менее 300 – 350 км обычно используют упрощенные Т- и П-образные схемы замещения с сосредоточенными параметрами. При этом погрешности электрического расчета линии практически зависят только от её длины. Выбор схемы замещения линии электропередачи определяется сложностью системы электроснабжения. При расчетах сложных систем электроснабжения на ЭВМ целесообразно использовать П-образную схему замещения с целью упрощения расчетов. Схемы замещения ЛЭП с сосредоточенными параметрами приведены на рис. 1.
В схемах замещения выделяют продольные элементы – сопротивления линии электропередачи: ? = ? + ?? и поперечные элементы – проводимости: ? = ? + ??. Значения указанных параметров для ЛЭП определяются по общему выражению П = П0?, где П0{?0, ?0, ?0, ?0} — значение продольного или поперечного параметра, отнесенного к 1 км линии; ? — протяженность линии электропередачи (погонные параметры).
В частных случаях, в зависимости от исполнения ЛЭП и класса напряжения, используют только доминирующие (наиболее характерные) параметры, в зависимости от их физического проявления.
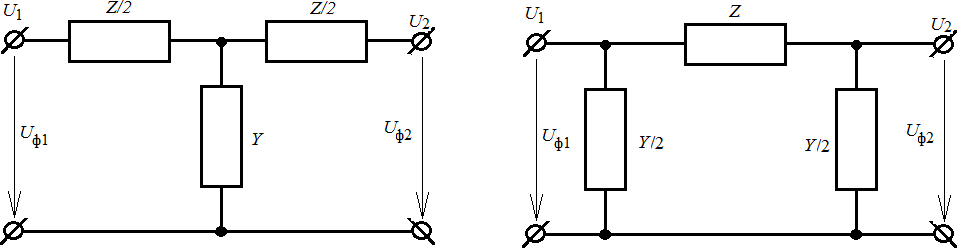
а) б)
Рис. 1. Схемы замещения ЛЭП с сосредоточенными параметрами: — Т – образная (а) и П – образная (б)
Активное сопротивление обуславливает тепловые потери и зависит от материала токоведущих проводников и их сечения. Для ЛЭП с проводами небольшого сечения из цветных металлов активное сопротивление принимают равным омическому, поскольку погрешности от неучета поверхностного эффекта на промышленной частоте в этом случае не превышают 1 %. Для ЛЭП с сечением проводов более 500 мм2 явление поверхностного эффекта на промышленной частоте значительно и его влияние необходимо учитывать.
Километрическое или погонное активное сопротивление (Ом/км) определяется по формуле
![]()
где ρ — удельное активное сопротивление металла провода, Ом ∙ мм2/км. Для технического алюминия в зависимости от его марки можно принять ρ = 29,5 ÷ 31,5 Ом ∙ мм2⁄км, для меди ρ = 18,0 ÷ 19,0 Ом ∙ мм2⁄км; ? – сечение фазного провода (жилы), мм2.
Необходимо помнить, что активное сопротивление зависит также от температуры провода, которая определяется температурой окружающей среды, скоростью ветра и значением протекающего по проводу силы тока.
Зависимость активного сопротивления от температуры провода t определяется соотношением
![]()
где ?020 – нормативное значение сопротивления ?0 – рассчитывается по соотношению ?0 = ρ/? при температуре проводника ? = 20℃; ? – температурный коэффициент электрического сопротивления, 1/град (для медных, алюминиевых и сталеалюминиевых проводов: α = 0,00403, для стальных – α = 0,00455).
Индуктивное сопротивление проводника X обусловлено магнитным полем, возникающим внутри и вокруг проводника при протекании по нему переменного тока. В проводнике наводится ЭДС самоиндукции
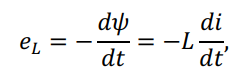
направленная в соответствии с принципом Ленца, противоположно ЭДС источника. Индуктивное сопротивление проводника ? зависит от частоты тока ω = 2π? и индуктивности фазы ?
![]()
Индуктивное сопротивление фаз многофазных ЛЭП зависит также от взаимного расположения фазных проводов (жил). Кроме ЭДС самоиндукции в каждой фазе наводится противодействующая ей ЭДС взаимоиндукции, значение которой в каждой фазе зависит от конструкции ЛЭП. Например, при расположении фаз по вершинам равностороннего треугольника результирующая противодействующая ЭДС во всех фазах одинакова и одинаковы пропорциональные ей индуктивные сопротивления фаз. При горизонтальном расположении фазных проводов потокосцепление фаз неодинаково, поэтому индуктивные сопротивления фазных проводов различны. Для достижения симметрии (одинаковости) параметров фаз ЛЭП высоких напряжений (500 кВ и выше) на специальных опорах выполняют транспозицию (перестановку) фазных проводов.
Индуктивное сопротивление, Ом/км, отнесенное к 1 км линии, на частоте тока 50 Гц и циклической частоте ω = 2π? = 314 рад/с, роводов из цветных металлов (магнитная проницаемость μ = 1) определяется по эмпирической формуле как сумма внешнего ![]() и внутреннего
и внутреннего ![]() индуктивных сопротивлений. Внешнее индуктивное сопротивление определяется внешним магнитным потоком, образованным вокруг проводов и значениями величин ?ср и ?пр. Внутреннее индуктивное сопротивление определяется внутренним потоком, замыкающимся в проводах.
индуктивных сопротивлений. Внешнее индуктивное сопротивление определяется внешним магнитным потоком, образованным вокруг проводов и значениями величин ?ср и ?пр. Внутреннее индуктивное сопротивление определяется внутренним потоком, замыкающимся в проводах.
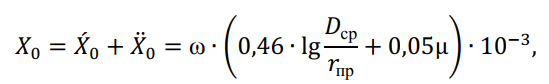
где ![]() — среднегеометрическое расстояние между фазными проводами (жилами), м;
— среднегеометрическое расстояние между фазными проводами (жилами), м;
![]() – радиус многопроволочных проводов, м;
– радиус многопроволочных проводов, м;
?ст – сечение стальной части провода;
? – суммарная площадь сечения токоведущей части многопроволочного провода;
μ – магнитная проницаемость материала, Гн/м.
При сближении фазных проводов влияние ЭДС взаимоиндукции возрастает, что приводит к уменьшению индуктивного сопротивления ЛЭП. Особенно заметно снижение индуктивного сопротивления (в 3 – 5 раз) в кабельных линиях. Разработаны компактные воздушные линии высокого и сверхвысокого напряжения повышенной пропускной способности со сближенными фазами с использованием эффекта взаимного влияния цепей и сниженным на 25 – 30 % индуктивным сопротивлением.
Из изложенного выше следует, что активное сопротивление линии электропередачи зависит от материала, сечения и температуры провода. Зависимость ?0 = ?(?) обратно пропорциональна сечению провода, ярко выражена при малых сечениях, когда ?0 имеет большие значения, и мало заметна при больших сечениях проводов. Индуктивное сопротивление ЛЭП определяется исполнением линии, конструкцией фазы и практически не зависит от сечения проводов (значение ![]() ).
).
Емкостная проводимость обусловлена емкостями между фазами, фазными проводами (жилами) и землей. В практических расчетах рабочую емкость трехфазной воздушной линии (ВЛ) с одним проводом в фазе на единицу длины, Ф/км, определяют по формуле
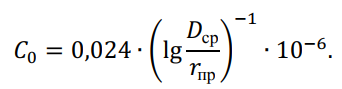
Аналогично определяется емкостная проводимость воздушной линии электропередачи, См/км
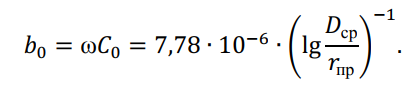
Под действием приложенного напряжения через емкости линий электропередачи протекают емкостные (зарядные) токи. Расчетное значение емкостной силы тока на единицу длины, кА/км
![]()
Зарядная мощность линии электропередачи, обусловленная током ??0, зависит от напряжения в каждой точке линии
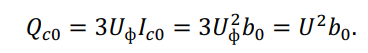
Значение зарядной мощности для всей ЛЭП определяется через действительные (расчетные) напряжения начала и конца линии, Мвар:
![]()
Зарядную мощность также можно приближенно определить по номинальному напряжению линии:
![]()
где ?? – емкостная проводимость ЛЭП, См; ?ном – номинальное напряжение ЛЭП, кВ.
ЛЭП с поперечной емкостной проводимостью, потребляющая из сети опережающий напряжение емкостной ток, следует рассматривать как источник реактивной (емкостной) мощности (зарядной мощности). Зарядная мощность уменьшает индуктивную составляющую нагрузки, передаваемую по линии к потребителю. Поэтому в схемах замещения ВЛ, начиная с номинального напряжения 110 кВ, следует учитывать поперечные ветви (шунты) в виде емкостных проводимостей ?? или реактивную мощность ??.
Для фаз ЛЭП напряжением 35 – 220 кВ выполненных одиночными проводами индуктивное сопротивление изменяется в узких пределах: ?0 = (0,4 ÷ 0,44)Ом/км, а емкостная проводимость находится в пределах ?0 = (2,6 ÷ 2,8)10−6 См/км.
Среднее значение зарядной мощности на 100 км для ВЛ напряжением 110 кВ составляет около 3,5 Мвар, для ВЛ 220 кВ – 13,5 Мвар, для ВЛ 500 кВ – 95 Мвар.
Активная проводимость обусловлена потерями активной мощности ∆?? из-за несовершенства изоляции (утечки по поверхности изоляторов, токов проводимости в материале изолятора) и ионизации воздуха вокруг проводника вследствие коронного разряда. Удельная проводимость определяется по общей формуле для шунта, См/км
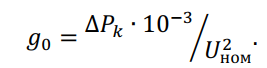
Доминирующими являются потери на коронирование, которые возникают только при достижении критической напряженности электрического поля у поверхности провода, кВ/см, определяемой по формуле:
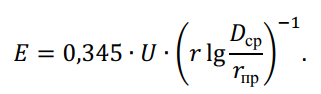
Значение критической напряженности составляет 17 – 19 кВ/см, что возможно только для ВЛ напряжением 110 кВ и выше. Для снижения потерь на корону до экономически приемлемого уровня ПУЭ установлены минимальные сечения (диаметры) проводов. Например, для ВЛ напряжением 110 кВ – АС 70 (11,8 мм), для ВЛ 220 кВ – АС 240 (21,6 мм).
2. Схемы замещения ВЛ для расчетов симметричных режимов
При расчете симметричных установившихся режимов электроэнергетической системы схему замещения составляют для одной фазы, т.е. продольные параметры воздушной линии, полные комплексные сопротивления ? = ? + ?? изображают и вычисляют для одного фазного провода (жилы), а при расщеплении фазы – с учетом проводов в фазе и эквивалентного радиуса (диаметра) фазной конструкции ВЛ.
Емкостная проводимость ?? учитывает проводимости (емкости) между фазами, между фазами и землей и отражает генерацию зарядной мощности всей трехфазной конструкции в начале и конце линии:
![]()
Активная проводимость линии G, изображаемая в виде шунта между фазой (жилой) и точкой нулевого потенциала схемы (землей), включает суммарные потери активной мощности на корону (или в изоляции) трех фаз в начале и в конце линии:
![]()
Поперечные проводимости (шунты) ? = ? + ?? в схемах замещения можно не изображать, а заменять мощностями этих шунтов. Например, вместо активной проводимости показывают потери активной мощности в начале передачи
![]()
или в изоляции кабельной линии
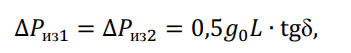
где L – длина линии электропередачи.
Взамен емкостной проводимости указывают генерацию зарядной мощности
![]()
Указанный учет поперечных ветвей ЛЭП нагрузками упрощает оценку электрических режимов, выполняемых вручную, поэтому такие схемы замещения называют расчетными. Схемы замещения воздушных линий электропередачи различных классов напряжения, в том числе с моделированием поперечных ветвей ЛЭП нагрузками показаны на рис. 2.
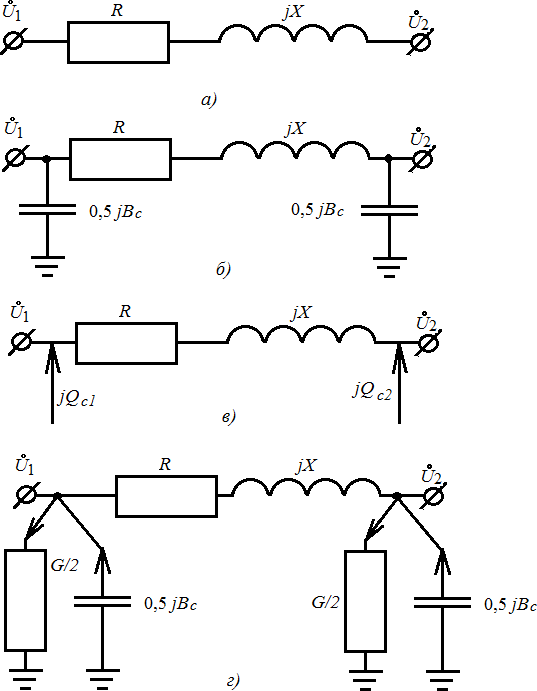
Рис. 2. Схемы замещения воздушных линий электропередачи: а) – ВЛ напряжением 0,38 – 35 кВ; б) – ВЛ напряжением 110 – 220 кВ с емкостными проводимостями; в) – ВЛ напряжением 110 – 220 кВ с зарядной мощностью вместо проводимостей; г) – ВЛ напряжением 330 (220) – 500 кВ с поперечными проводимостями.
Для линий до 220 кВ при определенных условиях можно не учитывать те или иные параметры, если их влияние на работу сети несущественно. В ВЛ напряжением до 220 кВ потери на корону незначительны, поэтому в расчете электрических режимов ими пренебрегают и соответственно принимают нулю активную проводимость.
Необходимость учета емкости и зарядной мощности линии зависит от соизмеряемости зарядной и нагрузочной мощности. В сетях до 35 кВ зарядные токи и мощности значительно меньше нагрузочных, поэтому в КЛ емкостную проводимость учитывают при напряжениях 20 и 35 кВ, а в воздушных линиях электропередачи ею можно пренебречь.
3. Схемы замещения ВЛ для расчетов несимметричных режимов
Токи нулевой последовательности воздушной линии возвращаются через землю и по заземленным цепям, расположенным параллельно длинной линии (защитные тросы, рельсовые пути вдоль линии и пр.). Точное токораспределение в земле в общем виде представляет весьма сложную задачу, поскольку распределение тока в земле выражается сложной закономерностью, аналогичной закономерности распределения тока в массивных проводниках. При этом плотность тока в земле наибольшая под проводом, как это показано на рис. 3.
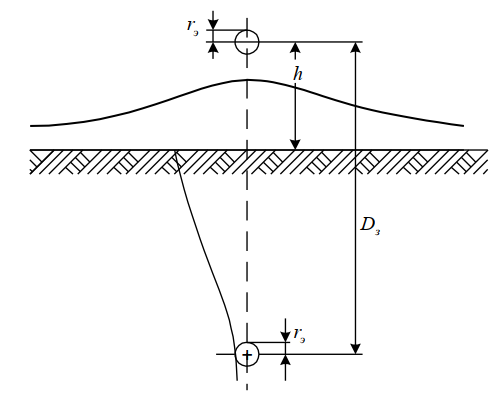
Рис. 3. Однородная линия «провод – земля».
Индуктивность линии «провод-земля», как показано Карсоном, может быть определена как индуктивность двухпроводной линии с расстоянием между проводниками Dз. Это расстояние называется эквивалентной глубиной возврата тока через землю и определяется по формуле Карсона, в метрах:
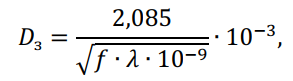
где — f – частота тока, Гц; λ – удельная проводимость земли, ![]() .
.
На частоте 50 Гц и среднем значении удельной проводимости земли ![]() , получим ?з = 935 м. При отсутствии данных о проводимости земли обычно принимают ?з = 1000 м. Тогда значение индуктивности линии «провод-земля» для токов нулевой последовательности
, получим ?з = 935 м. При отсутствии данных о проводимости земли обычно принимают ?з = 1000 м. Тогда значение индуктивности линии «провод-земля» для токов нулевой последовательности
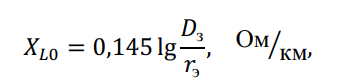
где rэ – эквивалентный радиус провода, значения которого составляют:
- для витых медных проводников в зависимости от числа прядей:
![]()
- для алюминиевых и сталеалюминиевых проводов марок А, АС, АСО, АСУ значение эквивалентного радиуса провода определяется с учетом соотношения:
![]()
где r – истинный радиус провода.
Для линии с расщепленными проводами вместо ?э берут средний геометрический радиус системы проводов одной фазы:
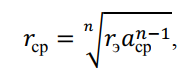
где n— число проводов в фазе; ?ср – среднее геометрическое расстояние между проводами одной фазы.
Активное сопротивление линии «провод – земля» складывается из активного сопротивления провода ?п и дополнительного сопротивления ?з, учитывающего потери активной мощности в земле от протекающего в ней тока:
![]()
которое при ? = 50 Гц дает ?з = 0,05 Ом⁄км, что свидетельствует о практическом постоянстве потерь активной мощности в земле при заданной частоте.
Сопротивление, обусловленное взаимоиндукцией между двумя параллельными линиями «провод-земля» с расстоянием ? ≪ ?з между осями их проводов:
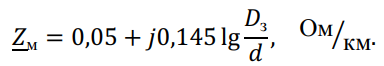
После преобразований получим выражение для расчета сопротивления нулевой последовательности:
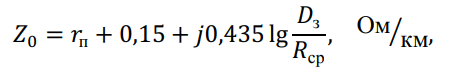
где — ![]() – средний геометрический радиус системы трех проводов линии;
– средний геометрический радиус системы трех проводов линии;
![]() – среднее геометрическое расстояние между фазными проводами фаз А, В, С.
– среднее геометрическое расстояние между фазными проводами фаз А, В, С.
Из изложенного следует, что взаимоиндукция с другими фазами уменьшает сопротивление фазы для токов прямой (обратной) последовательности и увеличивает его для токов нулевой последовательности. Взаимосвязь между сопротивлениями взаимной индуктивности, прямой и нулевой последовательностей ВЛ определяется соотношениями:
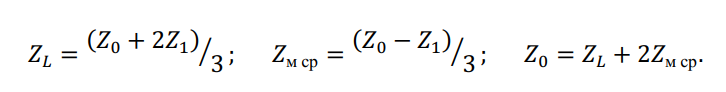
По каждой цепи двухцепной линии токи нулевой последовательности протекают в одном направлении, поэтому ?0 каждой из двух цепей увеличивается за счет взаимоиндукции и определяется по известной схеме замещения двух магнитосвязанных цепей, как показано на рис. 4. При идентичности параллельных цепей ??0 = ???0 = ?0 сопротивление нулевой последовательности каждой из них будет: ?0′ = ?0 + ??−?? 0, а сопротивление на фазу двухцепной линии:
![]()
Наиболее сильно увеличение сопротивления нулевой последовательности вследствие взаимоиндукции сказывается при расположении обеих цепей на одной опоре. Если расстояние между цепями порядка 400÷500 м, то увеличение Z0 не превышает 10 %.
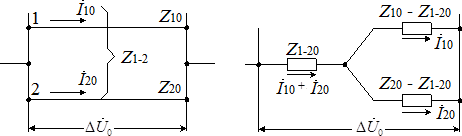
а) б)
Рис. 4. Двухцепная линия передачи (а) и ее схема замещения (б) нулевой последовательности
При наличии грозозащитного троса заземленного на каждой опоре индуктивное сопротивление нулевой последовательности линии снижается, а активное сопротивление нулевой последовательности сильно зависит от электрических параметров троса. Одноцепная линия с заземленным тросом и ее схема замещения показана на рис. 5. Сумма токов в тросе ?т и земле ?з̇ образуют ток в нейтрали, равной утроенному току нулевой последовательности в фазе линии. Тогда токи нулевой последовательности в тросе и земле будут:
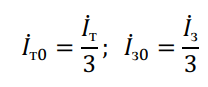
Для троса, как независимой однопроводной линии «провод-земля» можно записать выражение для индуктивного сопротивления:
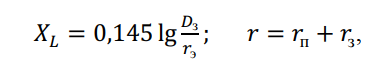
Чтобы учесть влияние токов всех фаз линии эти составляющие необходимо увеличить в 3 раза, что при частоте f = 50 Гц даёт:
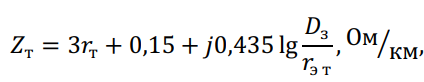
где ?т – активное сопротивление троса; ?эт – эквивалентный радиус троса.
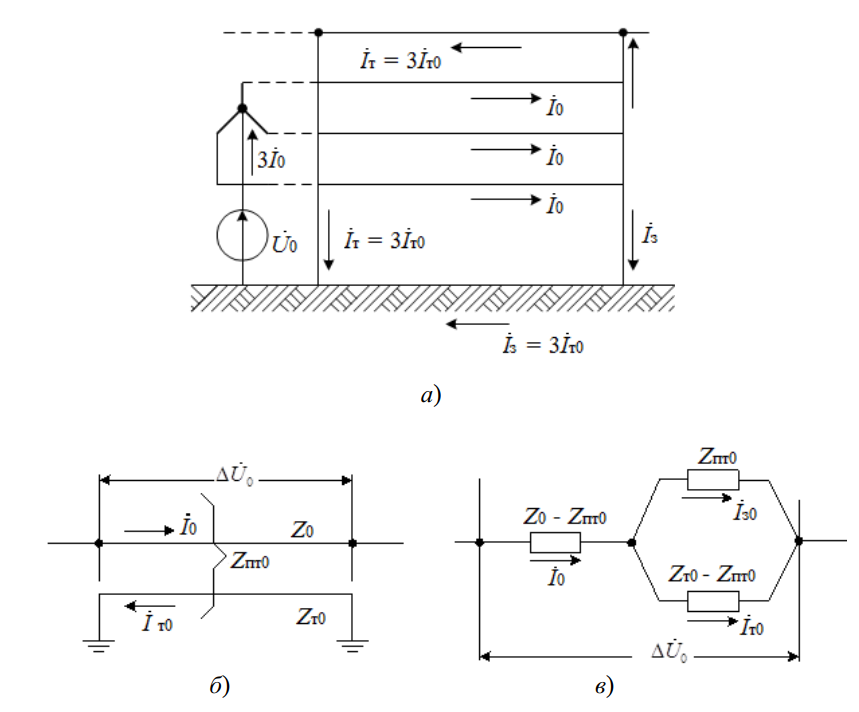
Рис. 5. Одноцепная линия с заземленным тросом: а – исходная принципиальная схема; б – исходная однолинейная схема; в – схема замещения нулевой последовательности
Сопротивление взаимоиндукции нулевой последовательности между проводом линии и тросом:
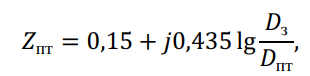
где ![]() – среднее геометрическое расстояние между фазными проводами фаз А, В, С и тросом.
– среднее геометрическое расстояние между фазными проводами фаз А, В, С и тросом.
По известным сопротивлений нулевой последовательности переходим от схемы (рис. 30,б) с магнитной связью между цепями к схеме замещения на рис. 30,в, результирующее сопротивление которой даёт искомое сопротивление нулевой последовательности с учётом заземлённых тросов:
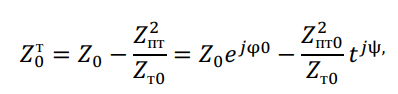
где ψ = 2φпт0 − φт0.
Значения аргументов сопротивлений в приведенном выражении находятся в пределах:
- при проводниках из цветных металлов φ0 = 75 ÷ 80°;
- при стальных проводниках – φт0 = 30 ÷ 45°;
- при расстоянии ?пт ≤ 100м значение φпт0 = 70 ÷ 80°.
По схеме замещения рис. 30,в, можно установить взаимосвязь между токами:
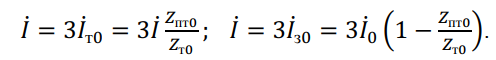
В приближённых практических расчётах в качестве средних соотношений между индуктивными сопротивлениями нулевой и прямой последовательностей принимают значения, указанные в табл. 1:
Таблица 1.
| Характеристика линии | Отношение х0 / х1 |
| 1. Одноцепная линия без тросов | 3.5 |
| 2. То же со стальными тросами | 3.0 |
| 3. То же с хорошо проводящими тросами | 2.0 |
| 4. Двухцепная линия без тросов | 5.5 |
| 5. То же со стальными тросами | 4.7 |
| 6. То же с хорошо проводящими тросами | 3.0 |
Реактивное ёмкостное сопротивление провода ВЛ (поперечное на 1 км) определяется по следующим выражениям:
- для прямой (обратной) последовательности без учёта влияния земли:
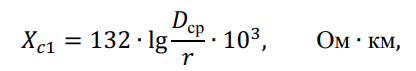
где r – радиус провода; ?ср – среднее геометрическое расстояние проводами фаз;
- для нулевой последовательности:
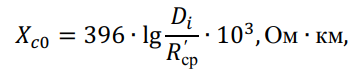
где ?ср′ — средний геометрический радиус систем трех проводов линии;
![]() – среднее расстояние проводов фаз А, В и С до их зеркальных отображений относительно поверхности земли; ℎ?, ℎ?, ℎ? − высоты подвеса проводов фаз относительно земли.
– среднее расстояние проводов фаз А, В и С до их зеркальных отображений относительно поверхности земли; ℎ?, ℎ?, ℎ? − высоты подвеса проводов фаз относительно земли.
Заземленный трос заметно влияет только на емкостное сопротивление нулевой последовательности:
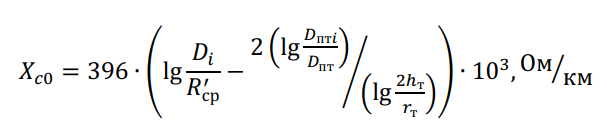
где ?т – радиус троса; ?пт – среднее геометрическое расстояние между проводами и тросом; ![]() – среднее расстояние между проводами фаз А, В, С и зеркальным отражением троса, подвешенного на высоте ℎт.
– среднее расстояние между проводами фаз А, В, С и зеркальным отражением троса, подвешенного на высоте ℎт.
Средние значения высоты подвеса нижнего провода зависят от значения напряжения (см. табл. 2) и составляют:
Таблица 2. Высота подвеса нижнего провода
| Напряжение, кВ | 35 | 110 | 220 | 330 | 500 |
| Высота подвеса нижнего провода, м | 8 | 9 | 10 | 15 | 15 |
Емкостное сопротивление всей линии определяется делением километрического емкостного сопротивления на полную длину линии в км.

